Graphing Linear Equalities
Solving Systems by Graphing
Writing Inequalities from Context
Testing Points in Inequalities
Optimization Station
100
What type of line (solid or dashed) do you draw for the inequality y > 2x + 1?
Dashed
100
What does the point of intersection represent in a system of linear equations?
A solution where the equations are true
100
Write an inequality for: “The number of tickets sold must be at least 500.”
x ≥ 500
100
Is the point (1, 3) a solution to y > x + 1?
Yes, because 3 > 1 + 1
100
What is the term for the region that satisfies all constraints in an optimization problem?
Feasible region
200
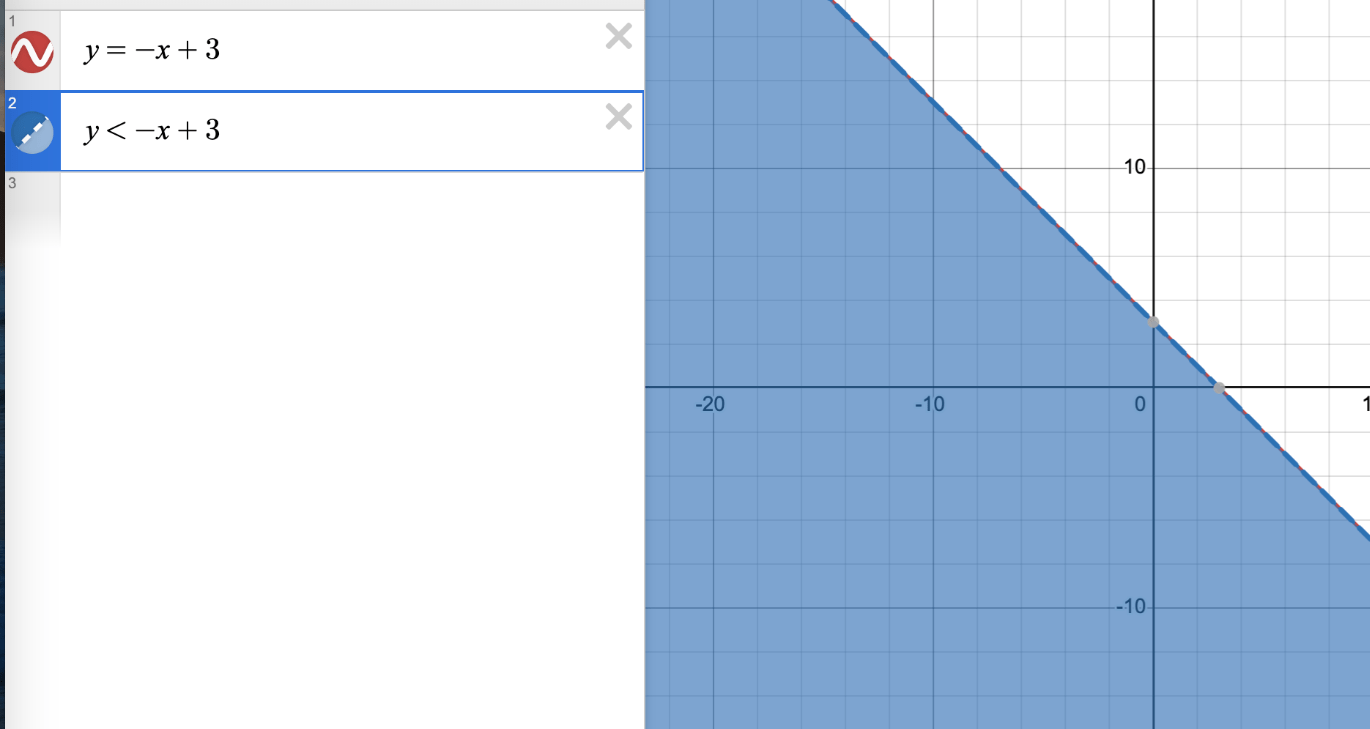
Which side of the line y = -x + 3 do you shade for the inequality y < -x + 3?
Test (0,0) -> 0<-0+3 -> 0<3 = True
200
Solve by graphing: y = -x + 2 and y = 2x - 1. What is the solution?
(1, 1) is the point of intersection and the solution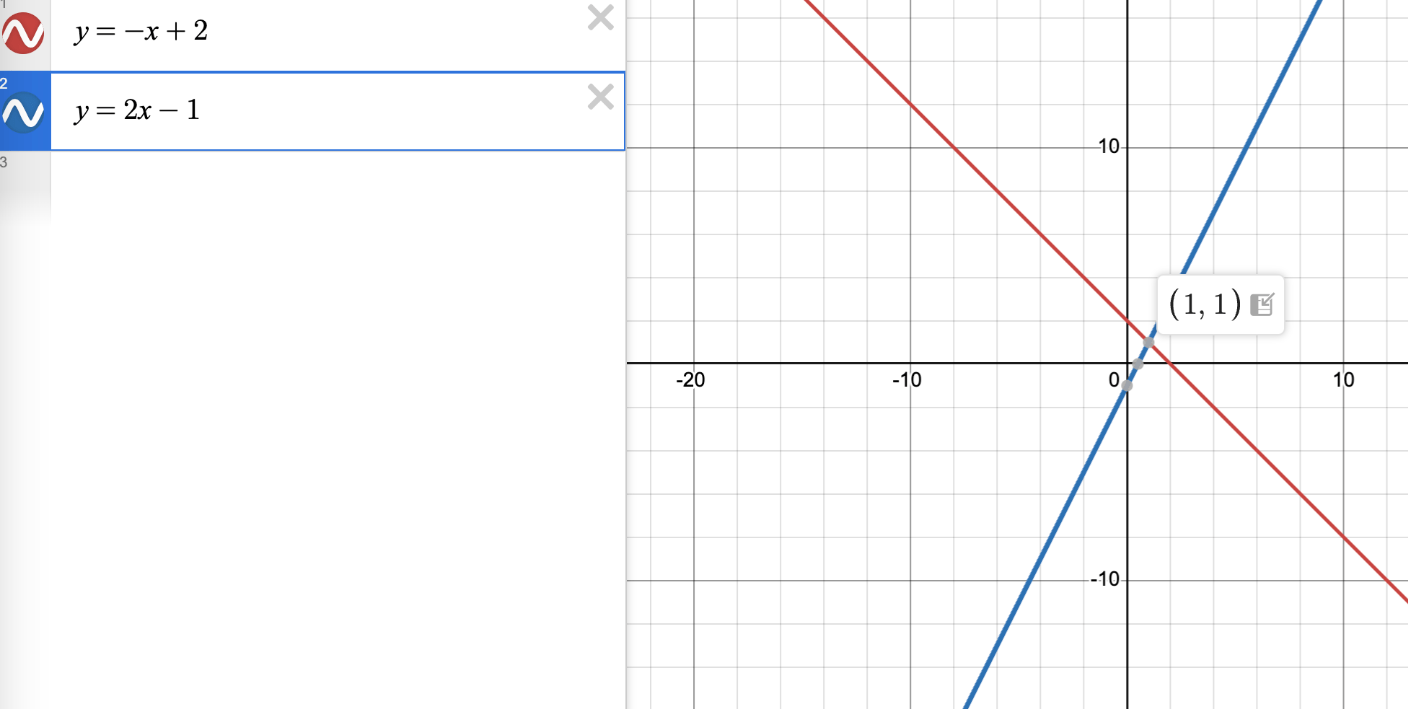
200
A vending machine holds no more than 240 cans. Write an inequality to represent this.
x ≤ 240
200
For the inequality 2x + 3y > 5, does the point (1, 0) satisfy it?
No, because 2(1) + 3(0) = 2, which is not greater than 5
200
What do we call the points where boundary lines intersect in a feasible region?
Corner points (vertices)
300
Based on the inequality 4x + 2y > -10. What is the slope and y-intercept of the boundary line?
Slope = -2
Y intercept = -5
300
If two lines intersect at (3, -4), does this point satisfy both equations: y = -2x + 2 and y = x - 7?
Yes, (3, -4) satisfies both equations when substituted
300
A football stadium sells at least 40,000 tickets per game. Represent this with an inequality using x.
x ≥ 40,000
300
Given y ≤ -2x + 4, test whether (2, 0) is in the solution region.
Yes, because 0 ≤ -4 + 4 → 0 ≤ 0
300
A company makes chairs and tables. Chairs take 4 hours to build, tables take 6. They have 48 hours and can make at most 6 tables. Write the constraints.
Constraints: 4x+6y≤48
y≤6
x,y≥0
400
Given the inequality 5x - 3y > 9, describe the steps to graph it and determine the solution region.
Rearranged: y < (5/3)x - 3; graph the line dashed,Test a point and shade a region
400
Graph the system: x + 2y = 6 and 2x - y = 2. What is the solution point?
Graphing both lines shows they intersect at (2, 2)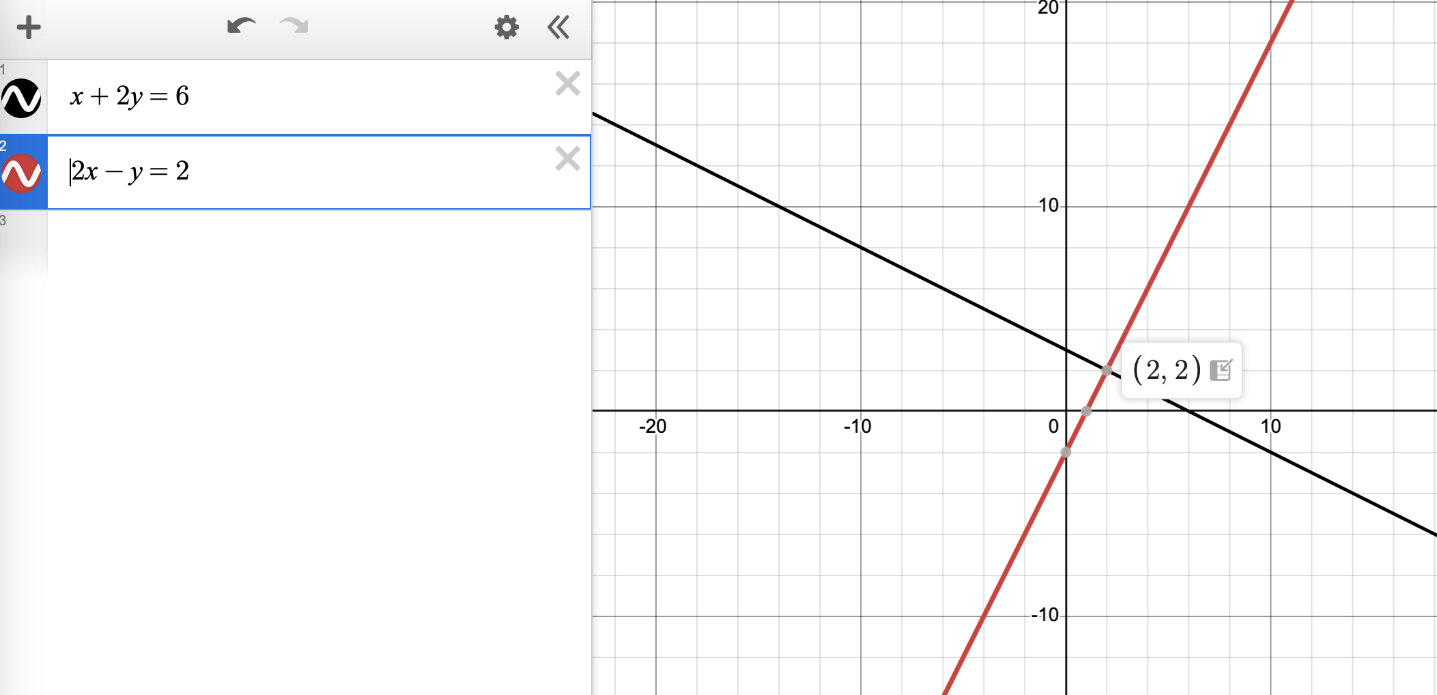
400
A parking lot has 540 m² available. Cars take 9 m², buses take 36 m². Write the inequality that models this situation.
9x + 36y ≤ 540, where x = cars and y = buses
400
A system includes y < x + 2 and y ≥ -x + 1. Is (0, 1) a solution to both?
Yes, (0, 1) satisfies both inequalities
400
You’re selling bracelets and necklaces. Bracelets earn $5 profit, necklaces earn $8. You can make up to 20 items total and must make at least twice as many bracelets as necklaces. What is the objective function and constraints?
Objective: P=5b+8n
Constraints: b+n≤20
b ≥ 2n
b,n ≥ 0
500
A system includes y ≤ -2x + 4 and y > x - 1. Sketch the solution region.
Left Side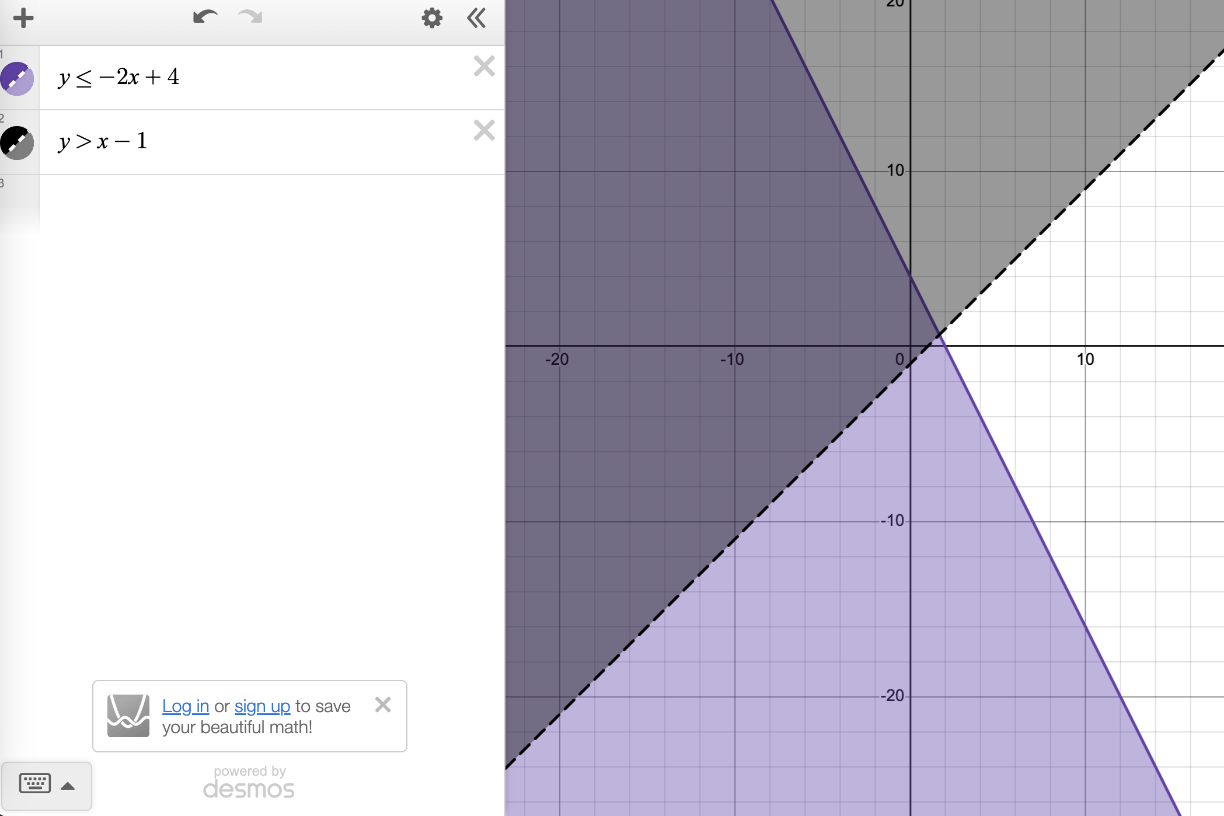
500
A system has no solution. What does this look like on a graph, and why does it happen?
The lines are parallel and never intersect—no solution
500
A food truck sells vegan meals for $10 each and non-vegan meals for $15 each. The truck can prepare no more than 120 meals in total per day and must not exceed a daily budget of $1,500. Additionally, the number of vegan meals sold must be at least twice the number of non-vegan meals. (Total of three constraints)
v+n≤120. (Total meals constraint)
10v+15n≤1500. (Budget constraint)
v≥2n. (Vegan meals must be at least twice non-vegan)
500
Without graphing, determine whether (3, -2) satisfies the system: 5x + 3y ≥ 9 and y < -2.
First inequality: 5(3) + 3(-2) = 15 - 6 = 9 → satisfies; Second: -2 < -2 → False, so not a solution
500
Given a feasible region bounded by three inequalities, how do you determine the maximum profit if profit is defined as P=3x+4yP = 3x + 4y?
Evaluate P=3x+4yP = 3x + 4y at each corner point of the feasible region and choose the highest value