What is the solution?

(-1,1)
Solve the systems of equations using substitution:
-3x + 4y = -2
y = -5
(-6, -5)
Solve the systems of equations using Elimination:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
What strategy would you use?
14x + 2y = 26
-14x - 6y = -50
Elimination
Is the given point a solution to the system of equations?
Point: (2,6)
x + y = 8
3x - y = 0
Yes
How many solutions are there?

No Solutions
Solve the systems of equations using substitution:
-5x - 5y = 10
y = -4x -17
(-5, 3)
Solve the systems of equations using Elimination:
-3x - 5y = 2
3x + 5y = 7
No Solution
If we add these equations together, both x and y are eliminated. Leaving us with 0 = 9, which is impossible
What strategy would you use? Bonus 200 points, if you can solve it!
-5x - 5y = 10
y = -4x -17
Substitution
Point of Intersection is (-5,3)
Is the given point a solution to the system of equations?
Point: (-2, -2)
6x + 5y = -7
2x - 4y = -8
No
However, (-2,1) is a solution
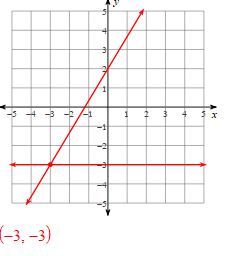
Solve Using Graphing:
y = 5/3x + 2
y = -3
Solve the systems of equations using substitution:
y = -2x - 9
3x -6y = 9
(-3, -3)
Solve the systems of equations using Elimination:
-6x - 10y = 4
6x + 10y = 0
No Solution
Is there 1 solution, No solution, or Infinite solutions for the system of linear equations below?
3x - y = 19
-3x + y = 10
No Solutions
What are the three types of Solutions we have learned about with Systems of Equations?
Draw an example of each, with correct labels
Infinite Solutions: Should be two lines that are the exact same
Zero Solutions: Two parallel lines that do not intersect
One Solution: Two lines that intersect at one point
How many solutions are there?
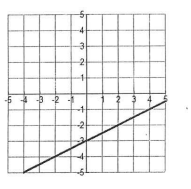
Infinitely Many Solutions
Solve the systems of equations using substitution:
-8x - 5y = -24
y = -x +10
(-2, 8)
Solve the systems of equations using Elimination:
3x + 24y = 66
3x + 4y = -14
(-10, 4)
How many solution would the following System of Equations have? No work required
2x - 4y = 12
2x + 14y = 23
They have the same slope, (the coefficient in front of x) they are parallel
Solve using Elimination
-3x +2y = 21
6x + 13y = 9
We first need to multiple the top equation by 2, making the coefficients of x opposite. Once we add them together we can solve for y, then x
(-5,3)
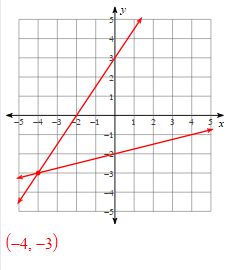
Solve the systems of linear equations by graphing:
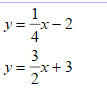
Solve the systems of equations using substitution:
8x + y = 7
16x +2y = 14
Infinitely Many Solutions
There are the same line, all that's different is that the second equation was multiplied by 2
Solve the systems of equations using Elimination:
-15x + 6y = -36
8x - 6y = 22
(2, -1)
How many solutions would the following Systems of Equations have?
5x - 13y = 1
10x -26y = 2
Infinite Solutions
They are the same line, because the second equation is just the first line multiplied by 2
Write two equations that have an infinite number of solutions. Everything must be correctly labeled
This is just my example, but there are an infinite number of options you can choose. But everything must be the same for both equations
y = 3x + 4 (Start at positive 4, place a point, go up 3 and one to the right, place the second point, connect)
y = 6x + 8 (Start at positive 8, place a point, go up six and one to the right, place the second point, connect)