Absolute Value Functions
Quadratic Functions
Transformations
Intervals and End Behavior
100
What is the vertex?
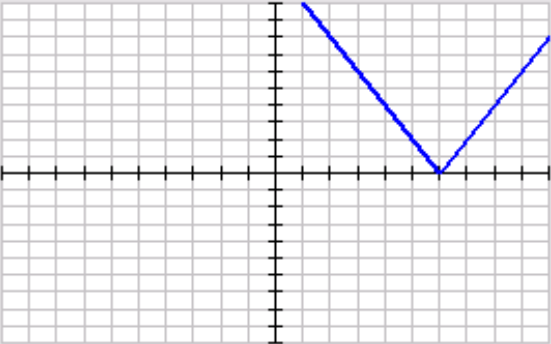
(6,0)
100
State the vertex of the function.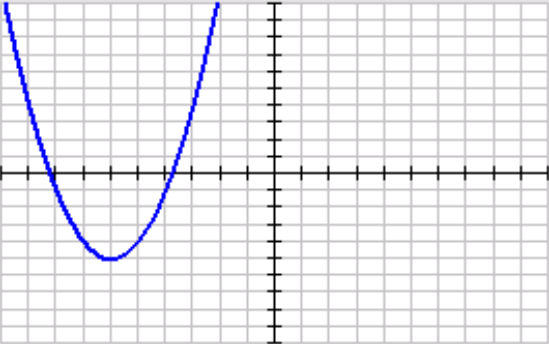
(-6, -5)
100
What is the transformation from the parent function?
f(x)=(x+7)^2
Shift left 7
100
What is the increasing interval for the function?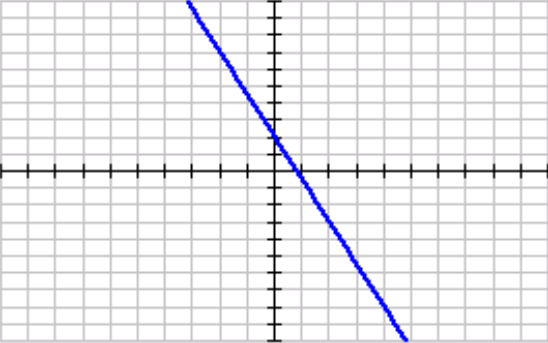
None
200
What is the domain?
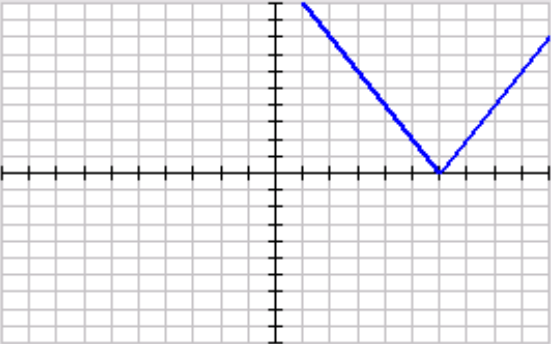
(-oo,oo)
200
State the axis of symmetry for the function.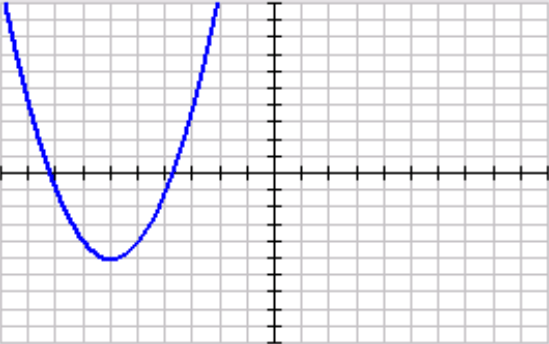
x=-6
200
What is the transformation from the parent function?
f(x)=-3/2x^2
Reflection, Vertical Stretch of 3/2
200
As. x ->oo, f(x)->
As. x ->-oo, f(x)->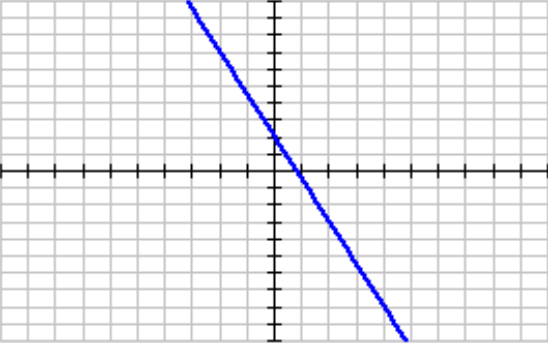
-oo
oo
300
State the domain and range of the function.
f(x)=-|x+1|+8
D: (-oo,oo)
R: (-oo, 8]
300
State the domain and range of the function.
f(x)=-2(x-3)^2+4
D: (-oo, oo)
R: (-oo, 4]
300
What is the transformation from the parent function?
f(x)=-2/3(x-1)^2+4
Reflection, Vertical Compression of 2/3, Right 1, Up 4
300
Over what interval is the function below decreasing?
f(x)=2(x+3)^2-5
(-oo, -3)
400
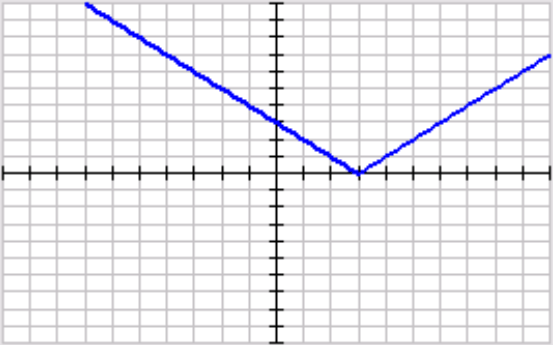
Graph the following function:
f(x)>|x-3|
Dotted, Shading Inside
400
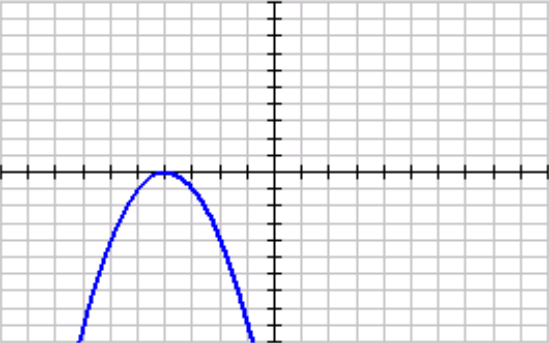
Graph the following function:
f(x)>=-(x+4)^2
Solid, Shading Outside
400
The graph of the absolute value parent function is vertically stretched by a factor of three, then shifted two units left and five units down. Write the new equation.
f(x)=3|x+2|-5
400
Given the function below, what describes the end behavior as x approaches positive infinity?
f(x)=(x+6)^2+2
oo
500
Write the function in vertex form.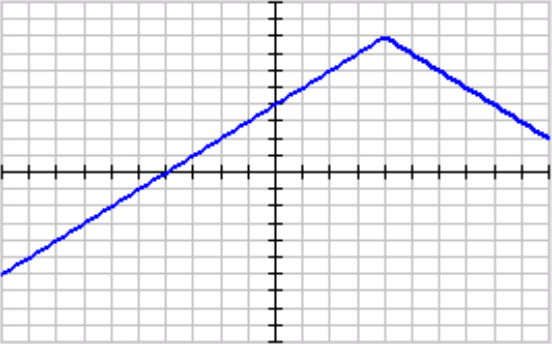
f(x)=-|x-4|+8
500
Write the function in vertex form.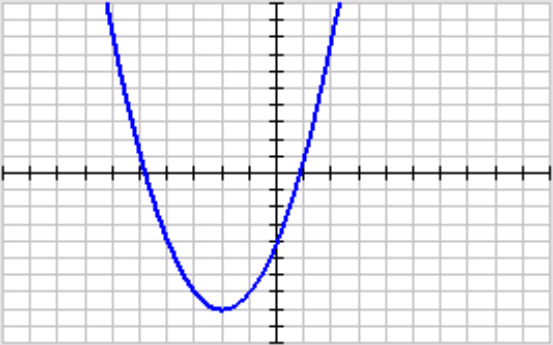
f(x)=(x+2)^2-8
500
The graph of the quadratic parent function is reflected across the x-axis, then shifted five units down and four units right. Write the new equation.
f(x)=-(x-4)^2-5
500
For the following function, state the increasing and decreasing intervals. Also state as x approaches infinity and negative infinity, what does f(x) approach?
f(x)=2(x-1)^2+4
Increase: (1,oo)
Decrease: (-oo,1)
As. x->oo, f(x) -> oo
As. x->-oo, f(x) -> oo