Inequalities
Lines in Triangles
Points of Concurrency
Vocabulary
100
Write an inequality to express the relationship between AB and BC.
AB > BC
100
What is AD if FD=5?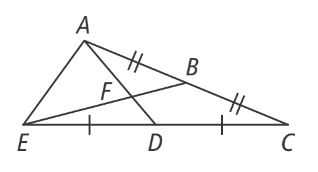
15
100
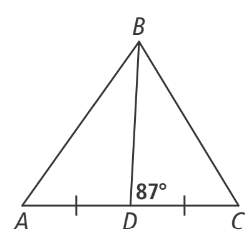
The orthocenter of △ABC is point B. What is the measure of ∠ABC?
90 degrees
100
Where do the three medians intersect?
Centroid
200
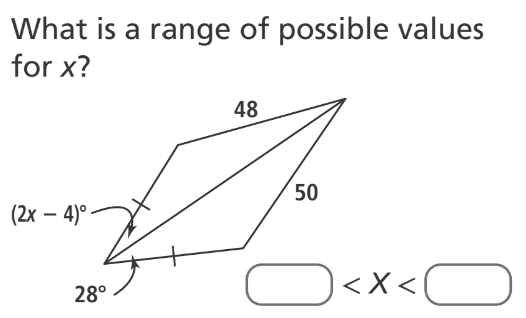
2<x<16
200
Suppose
BE=15x^2+3y
What is EF?
10x^2+2y
200
Select all the points that segment segment MO contains.
A. circumcenter
B. orthocenter
C. incenter
D. centroid
E. midpoint of side MN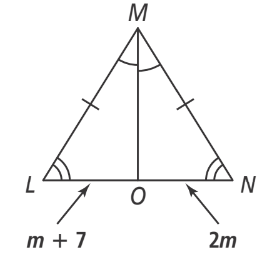
A. circumcenter
B. orthocenter
C. incenter
D. centroid
200
Where do the three perpendicular bisectors of a triangle intersect?
Circumcenter
300
Suppose AH < GB in the figure. Write an inequality that relates m∠ABH and m∠GHB.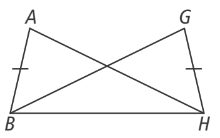
m∠ABH<m∠GHB
300
What is LN?
28
300
Using the points (1, 10), (−5, 2), and (7, 2) as vertices, where is the circumcenter?
(1, 15/4)
300
What line has end points at a vertex and and on the opposite side creating a right angle?
Altitude
400
A triangular frame has sides of length 18 in. and 27 in. What are the possible lengths (in whole inches) for the third side?
between 10 in. and 44 in.
400
Select all the descriptions for segment MO.
A. angle bisector
B. perpendicular bisector
C. median
D. altitude
E. hypotenuse
A. angle bisector
B. perpendicular bisector
C. median
D. altitude
400
Using the points (1, 10), (−5, 2), and (7, 2) as vertices, where is the orthocenter?
(1, 13/2)
400
Select all the true statements.
A. A circumcenter can be outside of its triangle.
B. An incenter can be outside of its triangle.
C. An orthocenter can be outside of its triangle.
D. A centroid can be outside of its triangle.
E. A circumcenter, orthocenter, incenter, or centroid can be either inside or outside of its triangle
A. A circumcenter can be outside of its triangle.
C. An orthocenter can be outside of its triangle.
500
Write an inequality for the possible values of x.
13<x<37
500
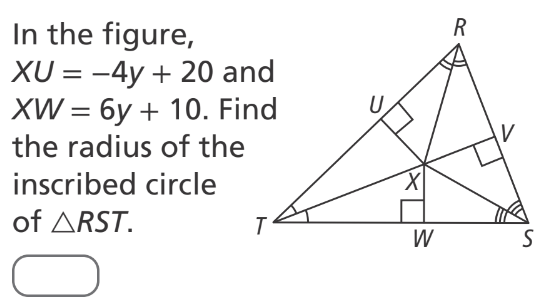
16
500
Using the points (1, 10), (−5, 2), and (7, 2) as vertices, where is the centroid?
(1, 14/3)
500
A police officer is parked at the junction of two streets. He wants to be equidistant from both streets. The police officer should be on the __________________.
Angle bisector