Given that a deluxe membership costs $500, then you pay $50 each month for your product, and a regular membership is $200 then you pay $65 per month for your product; What is the Independent Variable?
Number of months
Which of the following equations have the same slope?
a. 5y=2x+25
b. -6x+15y=75
c. -4x+10y=30
d. 2x+5y=15
a, b, and c.
What is the slope of the line containing the points (3,5) and (2,7)?
-2
Grandpa opened an account with $50 when you were born. He put some money in it each year for your birthday. When you were 7 there was $2150 in the account. When you were 13 there was $3950 in the account. Is the rate of change constant? If so, what is the slope?
Yes, it is constant. The slope is 300.
Given that a deluxe membership costs $500, then you pay $50 each month for your product, and a regular membership is $200 then you pay $65 per month for your product; Interpret what the slope of each line means.
The slope represents how additional money you would pay each month.
For the Deluxe membership the slope is 50, so you would pay an additional $50 each month. For the Regular membership you would pay an additional $65 per month.
What is the solution for these two equations and describe what the graph would look like.
a. 5y=2x+25
b. -6x+15y=75
Infinitely many solutions.
They would be the same line.
What does the b in the equation y=mx+b represent?
It is the starting value when you graph, or the y value of our y intercept.
Grandpa opened an account with $50 when you were born. He put some money in it each year for your birthday. When you were 7 there was $2150 in the account. When you were 13 there was $3950 in the account.
What is the meaning of the slope?
Given that a deluxe membership costs $500, then you pay $50 each month for your product, and a regular membership is $200 then you pay $65 per month for your product;
When, if ever would the two membership options cost you the same, and what would that cost be?
At 20 months the cost would be $1500 for either option.
What is the solution to this system of equations, and describe what the graph would look like.
a. 5y=2x+25
c. -4x+10y=30
No solutions, they are parallel. (or parallel lines with different y-intercepts)
What is the y-intercept for the equation of the line going through the points (3,5) and (2,7)
(0, 11)
Grandpa opened an account with $50 when you were born. He put some money in it each year for your birthday. When you were 7 there was $2150 in the account. When you were 13 there was $3950 in the account.
What is the y intercept and what is its meaning?
(0, 50) When you were born Grandpa put $50 into your account.
Given that a deluxe membership costs $500, then you pay $50 each month for your product, and a regular membership is $200 then you pay $65 per month for your product;
What is the y intercept of each equation and what is the meaning of that point?
(0,500) and (0,200) Just to sign up, the cost is either $500 or $200 depending on the option you choose.
What is the solution to this system of equations and what would the graph look like?
a. 5y=2x+25
d. 2x+5y=15
(-5/2, 4)
The lines have different slopes and would cross at the point (-5/2, 4)
What is the equation of the line going through the points (3,5) and (2,7)?
y=-2x+11
Grandpa opened an account with $50 when you were born. He put some money in it each year for your birthday. When you were 7 there was $2150 in the account. When you were 13 there was $3950 in the account.
What is the equation of the line modeling this?
A=300y+50
Given that a deluxe membership costs $500, then you pay $50 each month for your product, and a regular membership is $200 then you pay $65 per month for your product;
When would you want to choose the Deluxe option?
If you will be staying with the company at least 20 months.
What is the solution to the system of equations and what is significant about that point?
c. -4x+10y=30
d. 2x+5y=15
(0,3)
This point is contained in both lines, or this is where the lines cross. It is also the y intercept.
Graph the line going through the points (3,5) and (2,7).
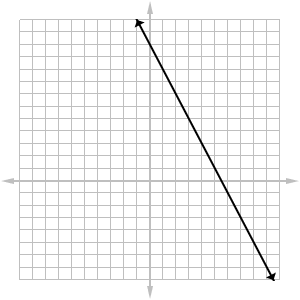
Grandpa opened an account with $50 when you were born. He put some money in it each year for your birthday. When you were 7 there was $2150 in the account. When you were 13 there was $3950 in the account.
How many years until you would have $8150 in your account?
27 years