True/ False
Fill in the Blank
Problems (go in order)
All About the Angles
Proof (go in order)
100
Lines are parallel only if they never meet.
True
100
A line that intersects two or more lines is called a _______________________.
Transversal line
100
Consider the following problem: In Triangle ABC, <A = 1/5 of a right angle, <B = 3/5 of a right angle.
What fact will help us to solve for <C?
The sum of the interior angles of a triangle equals 2 right angles.
100
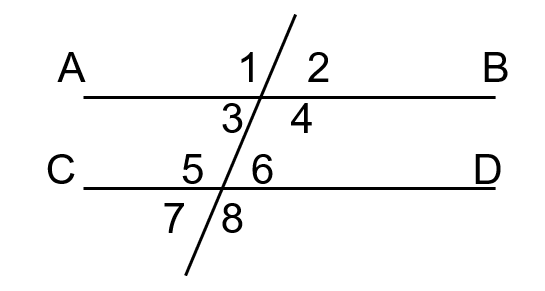Consider the figure on the left side of the board. What is the relationship between angles 6 and 7? What are they called?
Vertical Angles (equal)
100
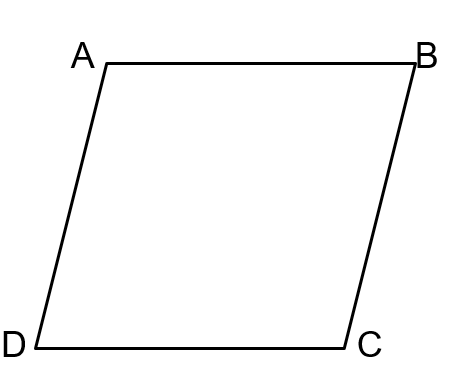
What is the definition of a parallelogram?
A quadrilateral with opposite sides parallel.
200
All corresponding angles are equal, whether the lines are parallel or not.
False
200
Triangles can be proved congruent using 4 methods: ______, ______, _______, and _________.
SAS
ASA
AAS
SSS
200
Consider the following problem: In Triangle ABC, <A = 1/5 of a right angle, <B = 3/5 of a right angle. All three angles add up to what fraction of a right angle?
<A +<B +<C = 10/5
200
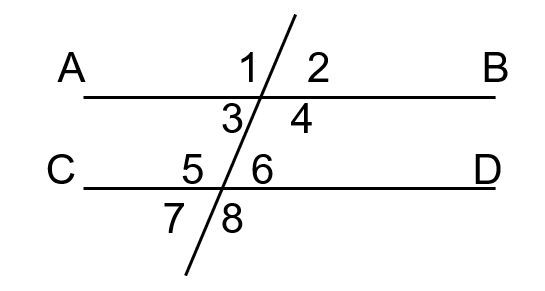Consider the figure on the left side of the board. What is the relationship between angles 5 and 6? What are they called?
Linear pair (supplementary)
200
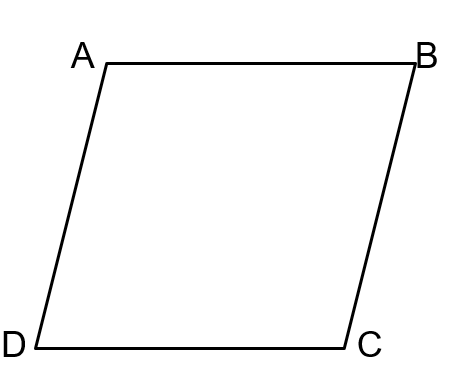
If we are trying to prove that AB = DC and AD = BC, we must first construct a diagonal. How do we know we can draw diagonal DB?
Postulate 1 (to draw a straight line from any point to any point).
300
If two triangles have 2 pairs of corresponding sides equal, then the third pair of sides must be equal.
False.
This is a fake SSS; we must be told that all 3 sides are equal in order for the triangles to be congruent.
300
The _______ of the interior angles of a triangle equals _______ right angles.
Sum
Two
300
Consider the following problem: In Triangle ABC, <A = 1/5 of a right angle, <B = 3/5 of a right angle. Find the measure of <C as a fraction of a right angle.
<C = 6/5
300
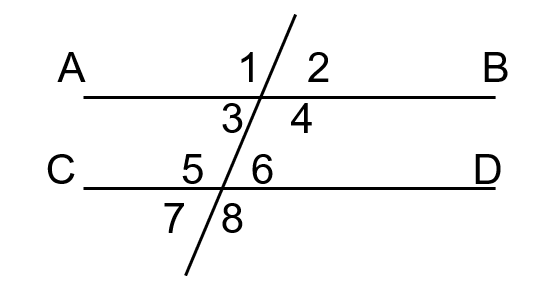Consider the figure on the left side of the board. What is the relationship between angles 1 and 5? What are they called?
Corresponding angles (equal)
300
Now that we have constructed a diagonal, we must prove what in order to prove that AB = DC and AD = BC?
Triangle ABD = Triangle CBD
400
A parallelogram is defined as having opposite sides equal.
False
It is defined as having opposite sides parallel! (:
400
Postulate ___ says that if a line falls on two lines making the interior angles on the same side less than _____ __________ _________ then the two lines when extended will meet on that same side.
5
two
right
angles
400
Consider the following problem: In Triangle ABC, <A = 1/5 of a right angle, <B = 3/5 of a right angle. To find the measure of <C in degrees, what must we multiply the fraction by?
90 degrees
400
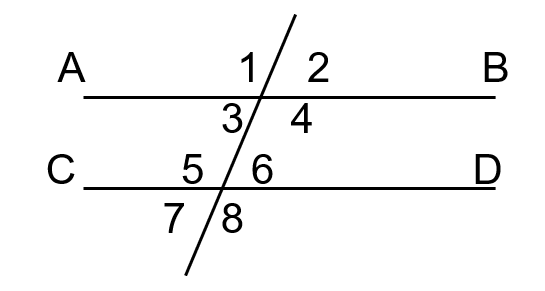Consider the figure on the left side of the board. What is the relationship between angles 4 and 5? What are they called?
Alternate interior angles (equal)
400
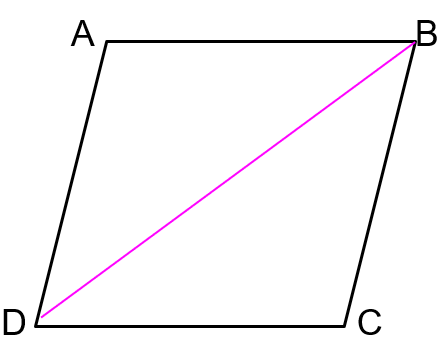
What types of angles must we take advantage of to prove Triangle ABD = Triangle CBD?
Alternate interior angles
500
When a line falls upon 2 lines making alternate interior angles equal, then the lines are parallel.
True!
Only if the lines are parallel will the alternate interior angles always be equal.
500
If line falls upon two parallel lines, it makes ______-______ _______ angles equal to two right angles.
Same
Side Interior
500
Consider the following problem: In Triangle ABC, <A = 1/5 of a right angle, <B = 3/5 of a right angle. Find the measure of <C in degrees.
108 degrees
500
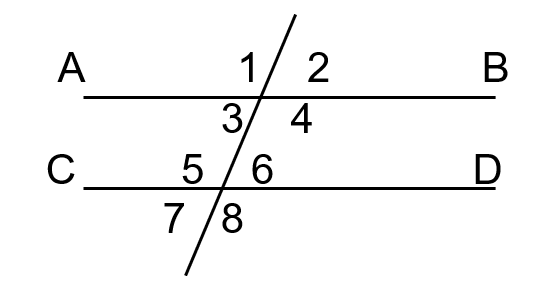Consider the figure on the left side of the board. What is the relationship between angles 4 and 6? What are they called?
Same-side Interior Angles (supplementary)
500
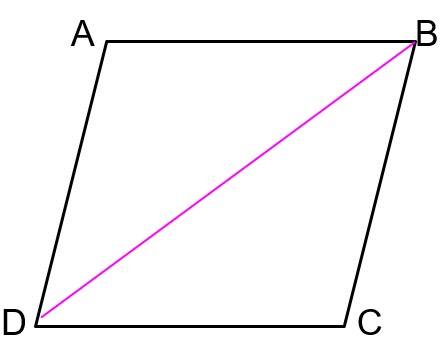
If DB is a common side, by what congruence theorem are Triangles ABD and CBD proven equal?
ASA