Find the measures of angles x and y.
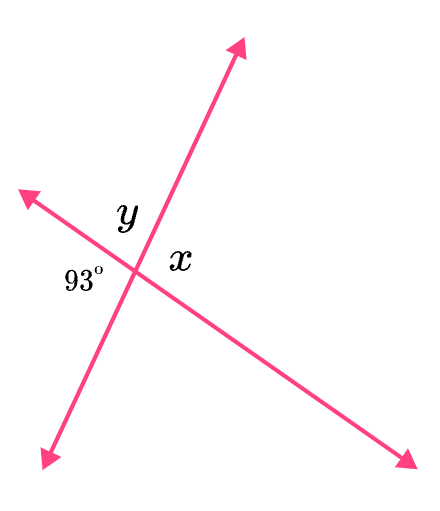
m\anglex=93^\circ
m\angley=180-93=87^\circ
180(13-2)=1980^\circ
How many multiples of 6 are between 24 and 115 inclusive?
24, 30,...,114
4, 5,...,19
1, 2,...,16
16 multiples of 6
I have 2 hats, 9 shirts, 5 pairs of pants, and 7 pairs of shoes. How many different outfits (one hat, one shirt, one pants, and one pair of shoes) can I make?
2*9*5*7=630 outfits
Evaluate \frac{2024!}{2023!}
\frac{2024!}{2023!}=\frac {2024*2023!}{2023!}=2024
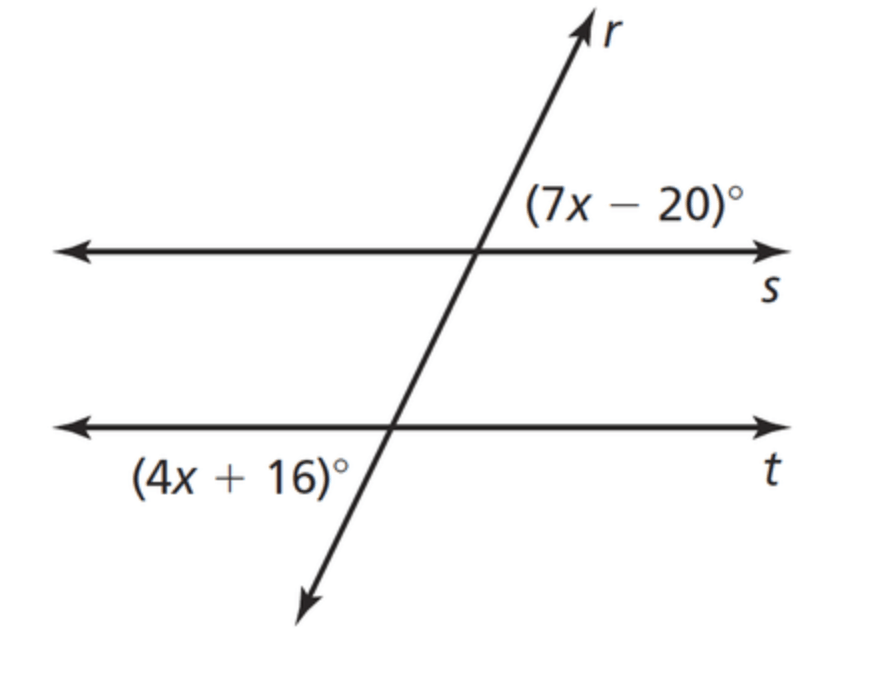 Find x if s||t
Find x if s||t
we have
7x-20=4x+16
3x = 36
x=12
How many sides does a polygon have if the sum of its interior angles is
9000^\circ ?
9000=180(n-2)
n=52
52 sides
How many numbers are in the following list?
8, 27, 64, 125,...,1000
Taking the "cube root" of each number yields:
2, 3, 4, 5,..., 10
Subtracting 1 from each number yields:
1, 2, 3, 4,...,9
A list which clearly contains 9 numbers.
Our basketball team has 12 members, each of whom can play any position. In how many different ways can I choose a starting lineup consisting of a center, a power forward, a shooting forward, a point guard, and a shooting guard?
12*11*10*9*8= 95040
Find
GCF(5!, 10!, 15!, 99!)
5! = 120
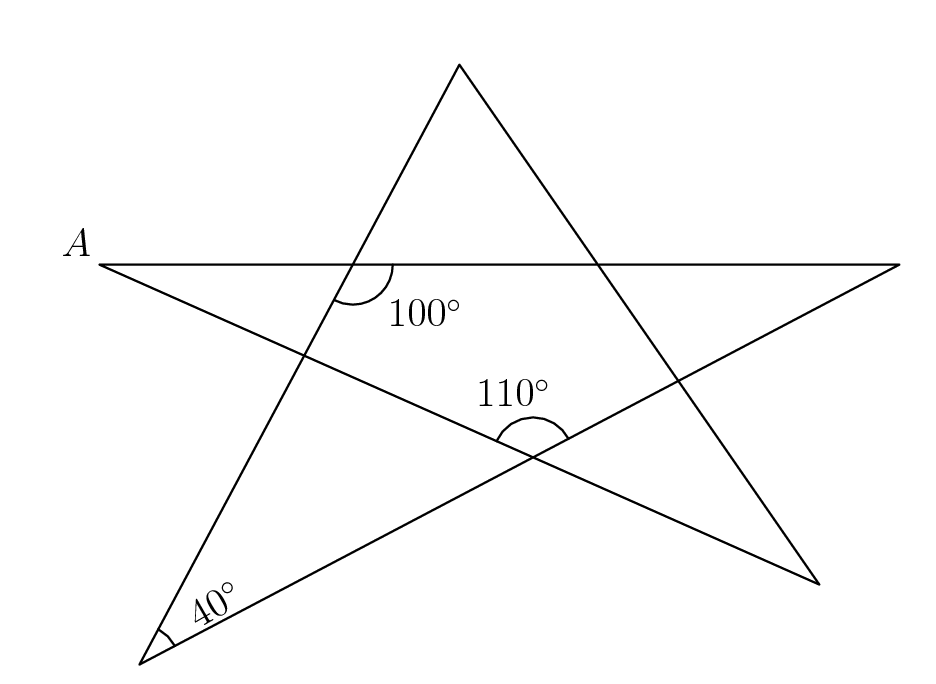 Find m\angleA
Find m\angleA
m\angleA=30^\circ
(use big or small triangles)
The measures of the interior angles of a pentagon are in the ratio 1:2:3:4:5. What is the measure (in degrees) of the second largest angle?
\frac{4}{15}=\frac{x}{540}
x = 144^\circ
Mr. Stewart's math class has 16 boys. 22 of his students brought a pencil to class. If 13 of the students who remembered a pencil are girls, how many boys forgot to bring a pencil?
22-13=9 boys remembered pencil. 16-9=7 boys forgot a pencil.
How many two-digit numbers have digits whose sum is a perfect square?
Case 1: Sum is 1
1 way (10)
Case 2: Sum is 4
4 ways (40, 31, 22, 13)
Case 3: Sum is 9
9 ways (90, 81, 72, 63, 54, 45, 36, 27, 18)
Case 4: Sum is 16
3 ways (97, 88, 79)
Total: 1+3+4+9 = 17
A club has 15 members, and needs to choose 2 members to be co-presidents. In how many ways can the club choose its co-presidents?
\frac{15*14}{2}=105 ways
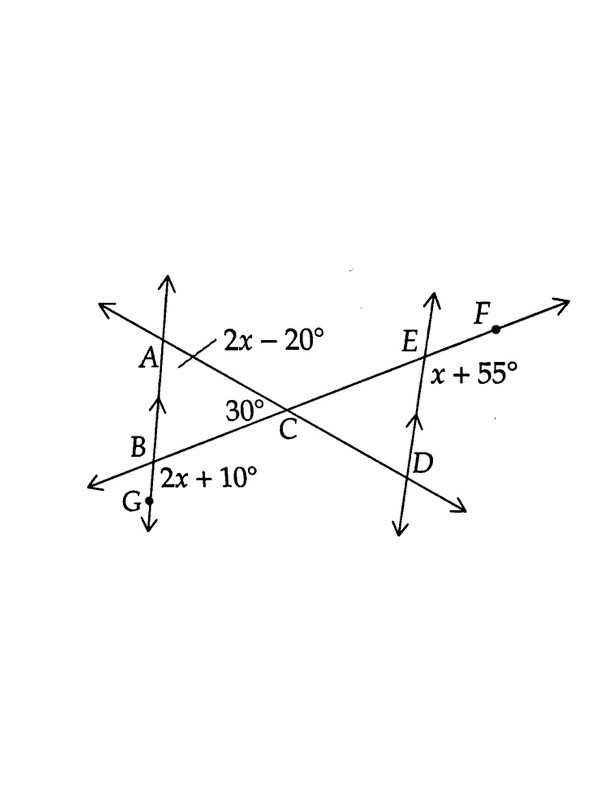
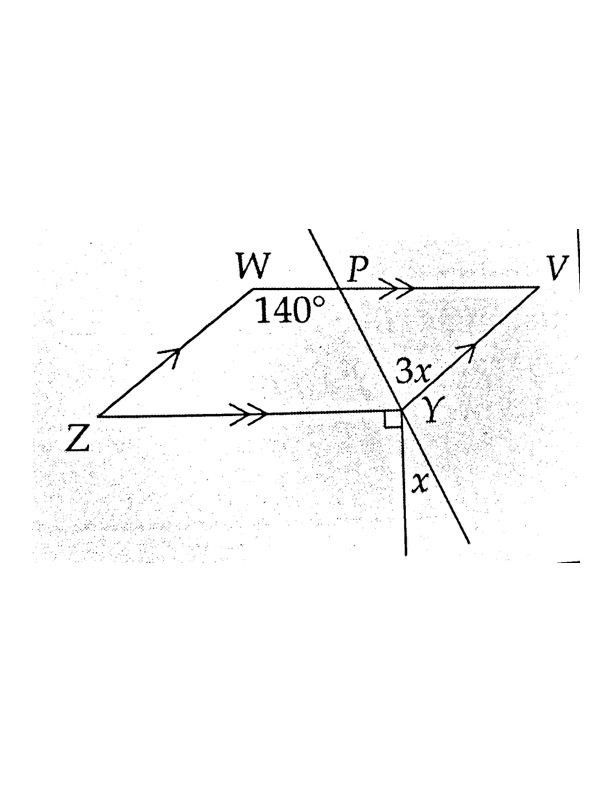 Find x if
Find x if
\overline{WV}||\overline{YZ}, \overline{WZ}||\overline{VY}
From parallel lines, x=25^\circ
Each exterior angle of a regular polygon measures
22.5^\circ
. How many sides does the polygon have?
360/n=22.5
n=360/22.5
n = 16
How many three-digit numbers are not multiples of 7?
772.
We count the three-digit multiples of 7:
105, 112,...,994
15, 16,...,142
1,2,...,128
Then, we subtract to find: 900-128 = 772
In how many ways can seven people be seated in a row if two of the people, Wilma and Paul, insist on sitting next to each other?
Treating Wilma & Paul as a unit, there are 6! ways to arrange the people. Then, Wilma and Paul have 2 possible orders within their unit, for a total of:
2*6! = 1440 ways.
How many diagonals (a line segment connecting two non-adjacent vertices) does a 23-gon have?
Each of the 23 vertices can have 20 diagonals drawn from it (to any vertex except itself and its neighbors). But, this counts every diagonal twice, for a total of
\frac{23*20}{2}=230 diagonals.
\overline{AB}||\overline{DE}
m\angleCED =?
m\angleCED=80^\circ
For how many whole-number values of n do the exterior angles of a regular n-gon have whole-number measures?
Hint: Use prime factorization, then a counting technique!
The sum of the exterior angles is 360, so we need
\frac{360}{n} to be a whole number (i.e. n|360).
Since 360=2^3*3^2*5 , we can "build" a prime factor of 360 using 0-3 2s, 0-2 3s, and 0-1 5s for a total of 4*3*2=24 divisors. However, we cannot have a 1 or 2 sided polygon, so only 22 values will work.
In my fencing club, there are twice as many boys who are in high school as there are boys who are in middle school. Of the students in the club who are in middle school, there are three times as many girls as there are boys. Half of the girls in the club are in high school. If there are 72 people in the fencing club, how many are middle school boys?
8 middle school boys.
How many 3-letter "words" have at least two consecutive letters that are the same?
Case 1: All 3 letters the same
26 ways (just choose the letter)
Case 2: Only 2 consecutive letters the same
2*26*25=1300 ways
Total: 1326 words
Find a formula for the sum of the first n even integers:
2+4+6+\cdots +2n
2+4+6+\cdots +2n=2(1+2+3+\cdots +n)
=2*\frac {n(n+1)}{2}
={n(n+1)}