Trig
Degrees/Radians
Quadrants
Co-terminals
Arc Length
100
Find the exact value of
cos(315o)
(root (2) 2)/2
100
convert 16π/3 to degrees
960
100
Determine the quadrant in which the terminal side of each angle θ will fall.
cos(θ) < 0 and π/2< θ <3π/2
Quadrant 3
100
Find(the closest) one negative and one positive coterminal angle
θ=7π/3
pi/3 and -(5pi)/3
100
What is the Arc Length formula given radians
radian x pi
200
Find the exact value of
tan (7π/6) =
(root (2)3)/3
200
convert 195° to radians
13/12pi
200
Determine the quadrant in which the terminal side of each angle θ will fall.
tan(θ) < 0 and sin(θ) > 0
quadrant 2
200
Find(the closest) one negative and one positive coterminal angle θ=300∘
660
-60
200
What is the arc length formula given degree
(degree)/360 x (2)x(r)x(pi)
300
Find the exact values of the remaining trigonometric functions of each angle θ .
cos(θ) < 0,tan(θ) = −4/7
Sin=
Cos =
sin = 4/root(2) 65
cos = -7/root(2)65
300
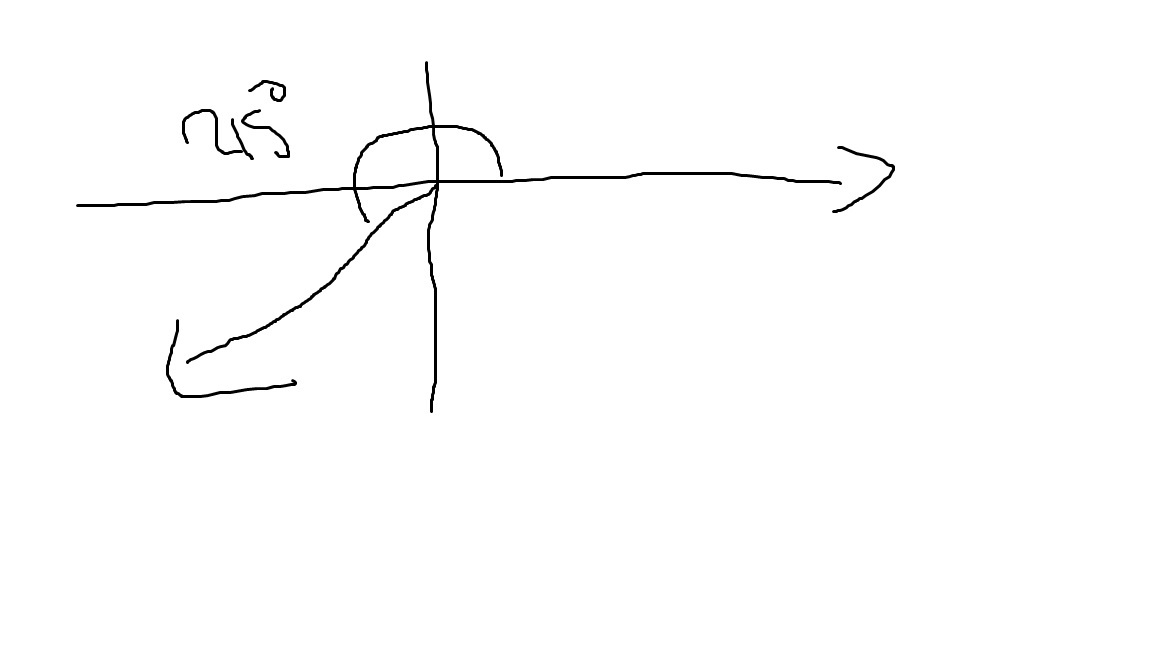
sketch Θ = 575°
300
Determine the quadrant in which the terminal side of each angle θ will fall.
tan θ > 0, π/2≤ θ ≤3π/2
Quadrant 3
300
Find(the closest) one negative and one positive coterminal angle θ=−405∘
315
-45
300
The diameter of a sector of a store floor is 16 yards long. The angle of sector is 184°.Determine the arc-length of the sector of the store floor in terms of π.
(368pi)/45
400
Find the values of the 3 trig functions of θ.
The point (8, -5) is on the terminal side.
(sin = -5/root(2)89 ) (cos = 8/root(2)89 )(tan =-5/8)
400
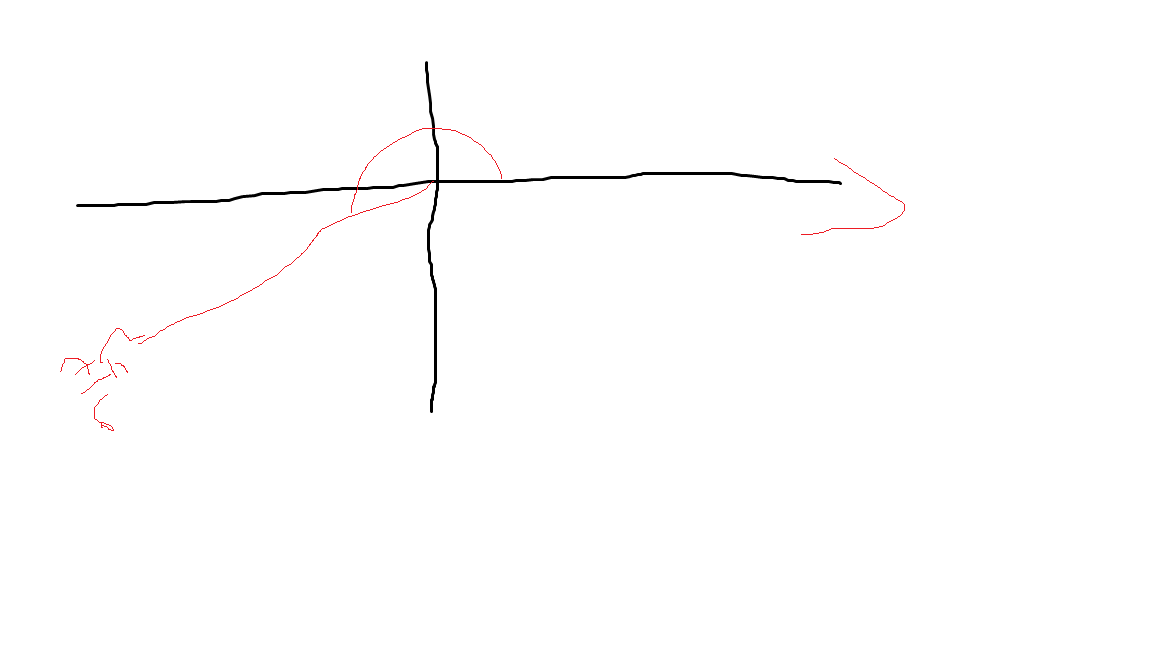
sketch
Θ =7π/6
400
Determine the quadrant in which the terminal side of each angle θ will fall.
tan θ > 0 and cos θ > 0
Quadrant 1
400
Find(the closest) one negative and one positive coterminal angle θ=−5π/7
(9pi)/7 (-19pi)/7
400
The radius of a sector of a carpet is 10 yards long. The angle of sector is 115°. Determine the arc-length of the sector of the carpet in terms of π.
(115pi)/18
500
Find the values for the remaining trig functions.
tan(θ) =5/14 , and π/2< θ < 3π/2
sin(θ) =
cos(θ) =
(sin = -5/root(2)221) (cos = -14/root(2)221)
500
What is the reference angle of 575 degrees
35
500
Determine the quadrant in which the terminal side of each angle θ will fall.
tanθ > 0, 3π/2≤ θ ≤5π/2
Quadrant 1
500
Find(the closest) one negative and one positive coterminal angle
θ=25π/6
(13pi)/6 -(11pi)/6
500
Suppose a sector has a central angle of θ =4π/3 and an arc length of 18π/7cm.Determine the length of the diameter.
27/7