Systems of Equations
Transformations of Quadratic Functions
Algebraic Skills with Quadratics (factoring)
Right Angle Trigonometry
Sine and Cosine Laws
100
2x + 2y = 6
3x - 5 = y
x = 2
y = 1
100
what kind of transformation happened here?
we subtracted 5 from the right side of the equation, so the graph shifted down 5
100
x2 + 16x + 64 =0
(x+8)(x+8)=0
x = -8; x=-8
100
tanB = opposite/adjacent = 9/5
B = 60.95o
100
Find the length of PQ using the sine law.
a/sinA = b/sinB a = b x sinA/sinB
PQ/sin48o = 18.3/sin27o
PQ = 18.3 x sin48o/sin27o
PQ = 29.96
200
x = 2y + 1
4x - 5y = 13
x = 7
y = 3
200
what kind of transformation happened here?
we added 2 to the right side, so the graph shifts 2 units up
200
x2 + 7x + 10 = 0
(x+2)(x+5) = 0
x=-2; x=-5
200
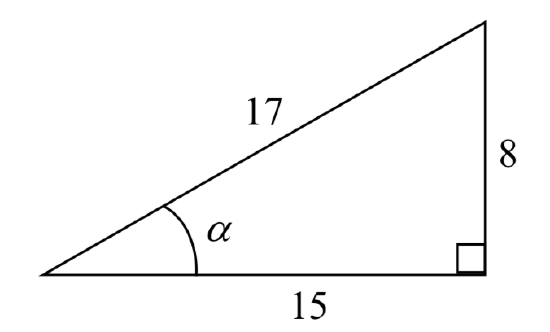
cos a = adjacent/hypotenuse = 15/17
a = 28.1o
200
find B in the triangle.
b2 = a2+c2 - 2ac cosB
9 = 25 + 36 - 60 cosB
9-61 = -60cosB
-52/-60 = cosB
cosB = 0.866667 B= 29.9o
300
2y = 4x
-3x + y = -4
x = 4
y = 8
300
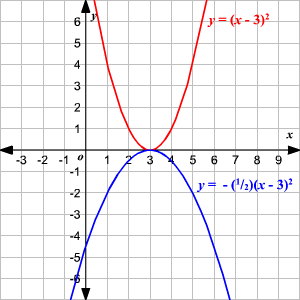
what happened to the graph here?
we multiplied the right side by −1/2 , so it turns the parabola upside down and gives it a vertical compression (or "squish") by a factor of 2.
300
x2 - 5x - 36 = 0
(x - 9)(x+4) = 0
x=+9; x=-4
300
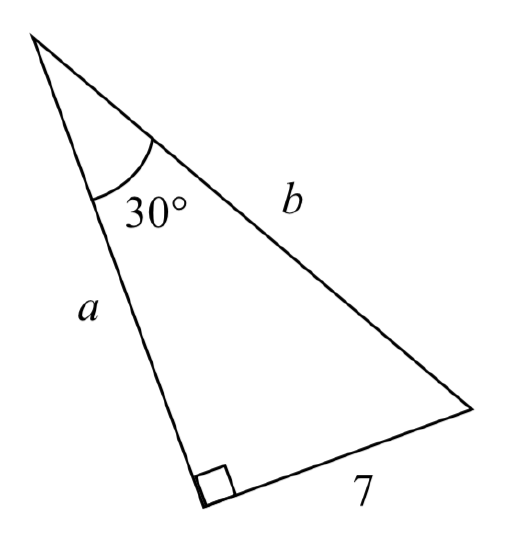
sin(θ)=opposite/hypotenuse
sin(30o)=7/b b = 14
a2+72=b2 a = √147
300
In triangle ABC, B = 21◦ , C = 46◦ and c = 9cm. Solve this triangle using the sine rule.
a/sin113o=b/sin21o=9/sin46o
b/sin21o=9/sin46o
b= sin21o x 9/sin46o = 4.484cm
a= sin113o x 9/sin46o = 11.517cm
400
3y = 12 - 6x
-15x - 4y =-2
x = -2
y = 8
400
Draw a graph that has shifted 3 units to the right from y=x2
we replaced x with (x-3)
400
12x2 + 13x + 3 = 0
(3x+1)(4x+3) = 0
x = -1/3; -3/4
400
A 10-foot pole has a rope attached to its top and stretched diagonally in a straight line to the ground. The angle of elevation from where the rope touches the ground looking up to the top of the pole is 50o. Find the length of the rope correct to two decimal places.
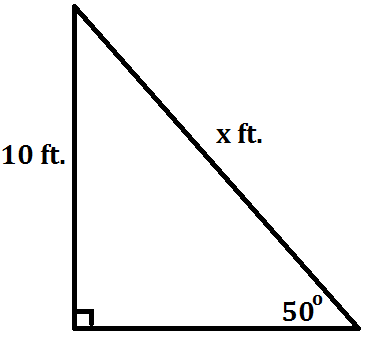
sin(50o)=10/x x=13.05
400
In triangle ABC, c = 42cm, a = 37cm and b = 26cm. Solve this triangle using the cosine rule.
372= 262 + 422 - 2(26)(42)cosA
cosA = 262 + 422− 372/(2)(26)(42) = 1071/2184 = 0.4904
A = cos-1 0.4904 = 60.63o
500
x = 1/2y - 7
3y = 42
x = 0
y = 14
500
draw what would happen if the graph y=x2 gets stretched vertically by a factor of 2
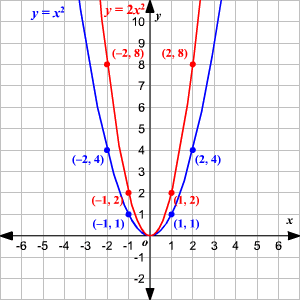
we multiplied the right side by 2
500
4x2 - 17x + 2 = -2
(x-4)(4x-1)=0
x=4; x=1/4
500
Sam is standing 20ft away from a large tree. The angle of elevation from her eyes, which are 5ft above the ground, to the top of the tree is 57o. How tall is the tree?
tan(57o) = x/20
x = 20tan(57o)
height of the tree: 20tan(57o) + 5 = 35.8ft
500
find the value of using the cosine rule.
c2 = a2+b2 - 2ab cos C
c2 = 82+112 - 2 x 8 x 11 x cos39o
c2= 64 + 121 - 176 cos39o
c2 = 48.22 c = 6.94