PROBLEM SET 1: Observing Patterns
Analyze each pattern
PROBLEM SET 2: Writing Expressions for Linear, Quadratic, and
Exponential Patterns
Exponential Patterns
Equivalent Expressions
PROBLEM SET 2: Writing Expressions for Linear, Quadratic, and
Exponential Patterns
Exponential Patterns
Sequences
100
Draw the next three terms for each pattern shown.
100
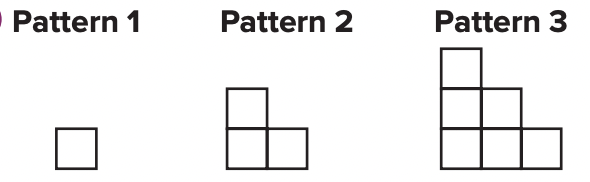
Determine the next number in each sequence. Explain your reasoning.
6, 13, 27, 55, .....
The next number in the sequence is 111. Each number in the sequence after the first number is two times the previous number plus one. So, the next number would be 2 ⋅ 55 + 1, or 111.
100
Renetta is creating a design for a craft project. Write an expression to represent the number of
shaded squares in each piece of the design.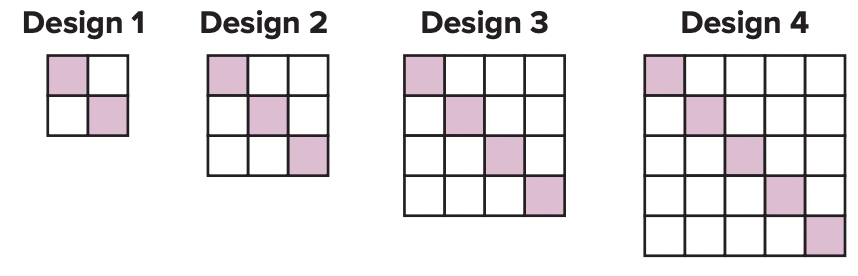
The number of shaded squares in each design is one more than the design number. So, the expression is n + 1.
100
6n + 8 and 2(3n + 4)
The expressions are equivalent. Use the Distributive Property. 2(3n + 4) = 6n + 8
100
The table lists the number of people who attended a museum (in thousands) over the course
of several months
The number of people who attended the museum is four times the number of months plus 7. So, an expression to represent the pattern is 4x + 7. The pattern is linear.
100
The school cafeteria begins the day with a supply of 1000 chicken nuggets. Each student that passes through the lunch line is given 5 chicken nuggets. Represent the total number of chicken nuggets remaining in the cafeteria’s supply after each of the first 6 students pass through the line with a numeric sequence. Include the number of chicken nuggets the cafeteria started with
Since the starting number is 1000 and the supply decreases by 5 per student, the remaining number of chicken nuggets starts at 1000 until the first student gets 5 of them, then what remains becomes 995. After the next student, the remaining number drops another 5 to 990, and so on. The resulting numeric sequence is 1000, 995, 990, 985, 980, 975, 970.
200
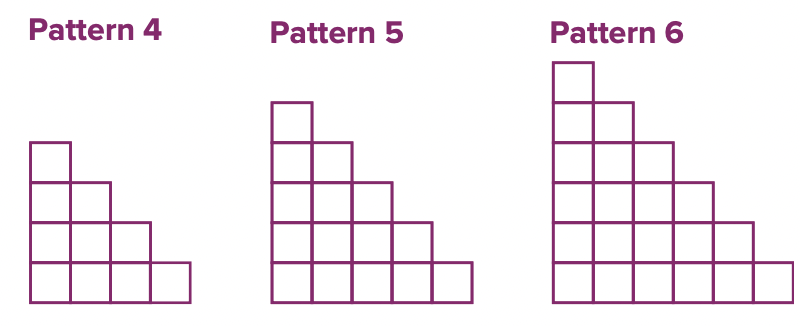
Draw the next three terms for each pattern shown.
200
Determine the next number in each sequence. Explain your reasoning.
1, 4, 7, 10, .....
The next number in the sequence is 13. Each number is the previous number plus three. So, the next number would be 10 + 3, or 13.
200
Three candidates for the student government each tell three other people that the election will be held next Tuesday. Those three people each tell three more people. Write an expression to model the number of people who hear the about the election being held next Tuesday
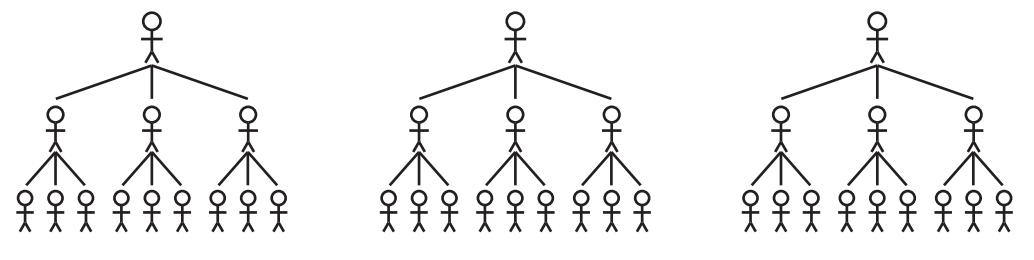
The number of people who hear about the election being held next Tuesday is 3x+1 , where x represents the number of tellings.
200
(n2 + 4n) − n2 and 4n
The expressions are equivalent. Combine like terms. (n2 + 4n) − n2 = n2 − n2 + 4n = 4n
200
A local pet shelter is able to see many of their pets adopted. The table lists the number of pets that have been adopted over several weeks.
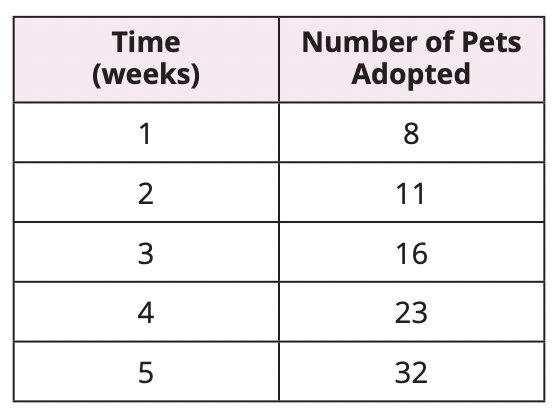
The number of pets adopted is the number of weeks squared plus 7. So, an expression to represent the pattern is w2 + 7. The pattern is quadratic.
200
Sophia starts a job at a restaurant. She deposits $40 from each paycheck into her savings account. There was no money in the account prior to her first deposit. Represent the amount of money in the savings account after Sophia receives each of her first 6 paychecks with a numeric sequence
0, 40, 80, 120
300
Draw the next three terms for each pattern shown.
300
Determine the next number in each sequence. Explain your reasoning.
3, 8, 18, 38
The next number in the sequence is 78. Each number is two times the previous number plus two. So, the next number would be 2 ⋅ 38 + 2, or 78.
300
Charlie watches as a pattern develops. He starts with 3 guppy fish in his fish tank. The next month, he finds 6 guppy fish in his tank. The following month, he finds 11 guppy fish in his fish tank. Write an expression to model the pattern of guppy fish in Charlie’s fish tank.
The number of fish that Charlie observes each month is the square of the month number, plus 2. So, the expression is n2 + 2.
300
15 − 6x and 15(1 − 6x)
The expressions are not equivalent. 15(1 − 6x) = 15 − 90x, which is not equivalent to 15 − 6x.
300
Emilio is looking at bunches of grapes at the market. He starts to notice a pattern in the
number of grapes in each bunch. The diagram shows the number of grapes in each bunch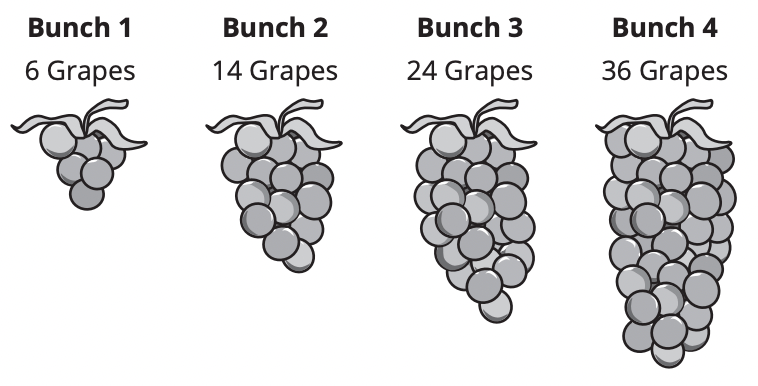
The number of grapes in each bunch is x squared plus 5 times x, where x represents the bunch number. So, an expression to represent the pattern is x2 + 5x. The pattern is quadratic.
300
Kyle is collecting canned goods for a food drive. On the first day, he collects 1 can. On the second day, he collects 2 cans. On the third day, he collects 4 cans. On each successive day, he collects twice as many cans as he collected the previous day. Represent the total number of cans Kyle has collected by the end of each of the first 7 days of the food drive with a numeric sequence.
400
Draw the next three terms for each pattern shown.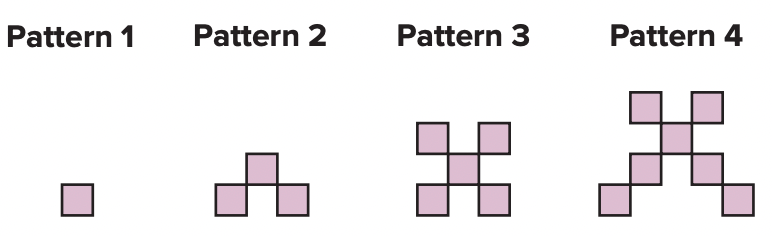
400
Determine the next number in each sequence. Explain your reasoning.
3, 5, 9, 17
The next number in the sequence is 33. Each number is two times the previous number minus one. So, the next number would be 2 ⋅ 17 − 1, or 33.
400
A library receives book donations over the course of the year. The number of books received
each month is listed in the table. Write an expression to model the number of books received
by the library.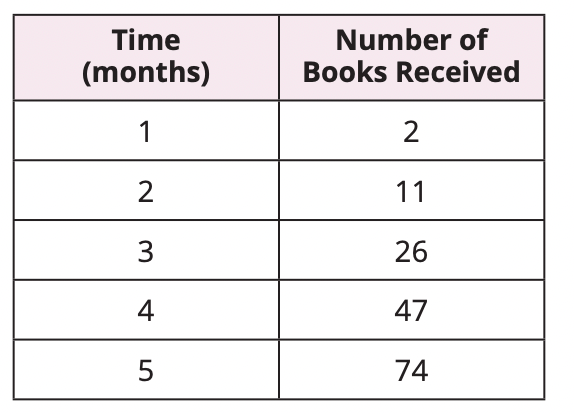
The number of books received is 3 times the number of months squared, minus 1. So, the number of books received in month n is 3n2 − 1.
400
(y + y + 2 + y) + 3y and 6y + 2
The expressions are equivalent. Combine like terms. (y + y + 2 + y) + 3y = 3y + 2 + 3y = 6y + 2
400
Nolan takes a photo of a parking lot every two hours. He counts the number of cars in each
photo. The diagram shows the number of cars in each photo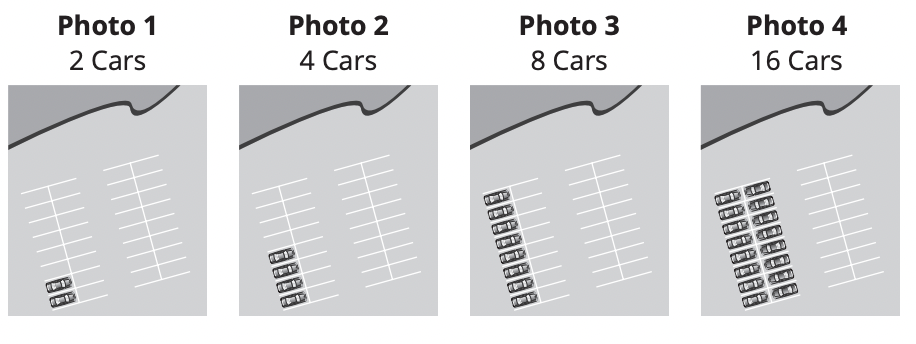
The number of cars in the parking lot in each photo is 2 to the power of x, where x represents the photo number. So, an expression to represent the pattern is 2x. The pattern is exponential.
400
Use an explicit formula to determine the unknown term in each arithmetic sequence.
Determine the 20th term of the sequence 1, 4, 7, ..
500
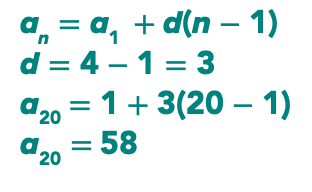
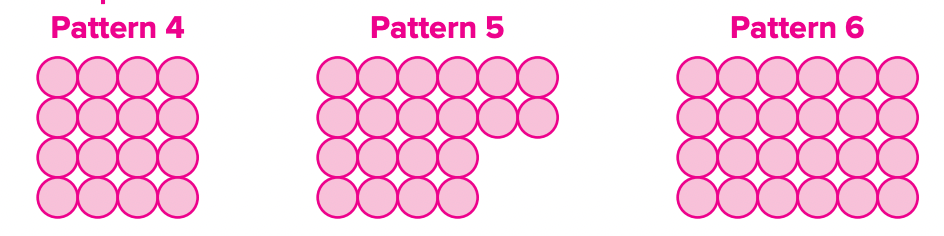
Draw the next three terms for each pattern shown.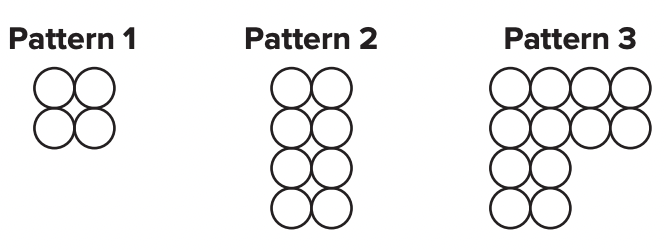
500
Determine the next number in each sequence. Explain your reasoning.
1, 5, 9, 13, ....
The next number in the sequence is 17. Each number is the previous number plus four. So, the next number would be 13 + 4, or 17.
500
A website begins its first week with 3 subscribers. The number of subscribers each week is listed in the table. Write an expression to model the number of subscribers at the website each week.
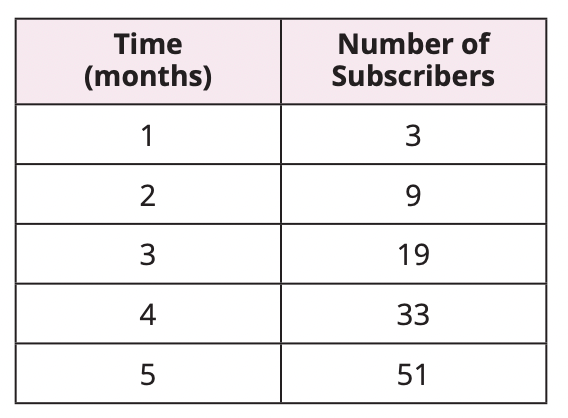
The number of subscribers is 2 times the number of weeks squared, plus 1. So, the number of subscribers in week n is 2n2 + 1.
500
8y − 3 + 10y and 3(6y − 1)
The expressions are equivalent. Combine like terms for the first expression. Use the Distributive Property for the second expression. 8y − 3 + 10y = 18y − 3 3(6y − 1) = 18y − 3
500
A store had a grand opening sale. During the sale, each person entering the store received a
coupon for 10% off their entire purchase. The table lists the number of people who received
a coupon.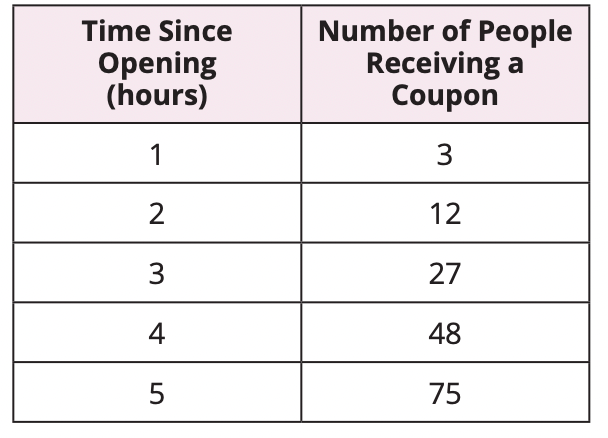
The number of people receiving a coupon is 3 times the square of the number of hours since opening. So, an expression to represent the pattern is 3x2. The pattern is quadratic.
500
Determine whether each sequence is arithmetic or geometric. Then, use the appropriate recursive formula to determine the unknown term(s) in the sequence
4, 8, 16, 32, _____, ...
