Key Concepts
Symmetry
What Happened?
Find the Point!
Congruency Statements
100
What type of transformation is represented below?
(x+3, y)
Translation right 3
100
How many lines of symmetry does a rectangle have?
2
100
What happened to map Triangle ABC to map onto Triangle ZXY?
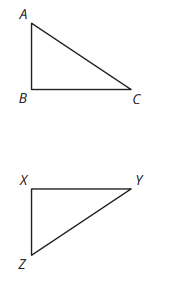
Reflect across BC and Translate it down from Point B to X.
100
Find point M when you rotate this figure 180 degrees.
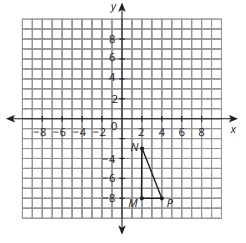
(-2,8)
100
Triangle ABC = Triangle XYZ
Which segment is congruent to AB?
Segment XY
200
What type of transformation is represented below?
(-x,y)
Relfection across y-axis
200
How many lines of symmetry does an Isosceles trapezoid have?
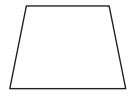
1
200
What happened from Triangle BDN to Triangle XZY?
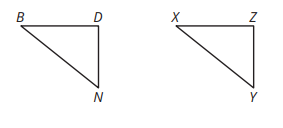
Translated right from Point B to Point X
200
Reflect the image across the x axis. Where will Point K end up?
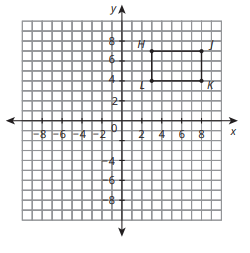
(8,-4)
200
Triangle ABC = Triangle HIJ
Which Segment is congruent to Segment AC?
Segmet HJ
300
What type of transformation is represented below?
(-y,x)
Clockwise 270 or Counterclockwise 90
300
How many lines of symmetry does a regular pentagon have?
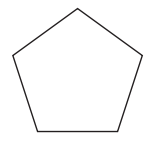
5
300
What happened to the following?
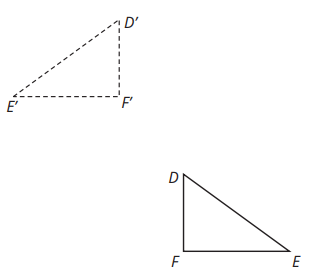
Reflect across DF and Translate from DD'
300
Rotate image 180 degrees, where will points W and Y end up
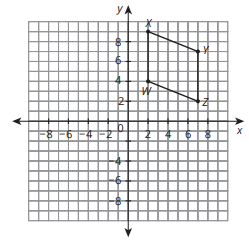
W'(-2,4) and Y'(-7,-7)
300
Triangle LMN = Triangle QRS
What angle is congruent to <NLM?
<SQR
400
Name all types of Isometry...
Reflection
Rotation
Translation
400
How many lines of symmetry does a regular hexagon have?
6
400
What happened?
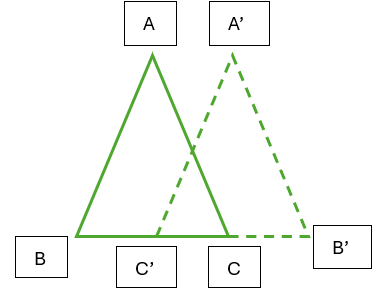
Reflected across vertical line equidistant between A and A'
400
Where will points A and C be after reflect across y axis and down 4?
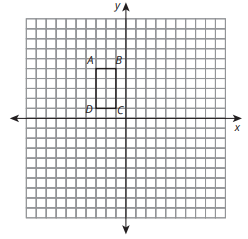
A'(3,1)
C'(1,-3)
400
Quadrilateral MATH = Quadrilateral EVIL
Which angle is congruent to <HMA?
<LEV
500
Which figure represents the Perpendicular Bisector theorem? 1st example or 2nd example? Must Explain Why to Gain Credit.
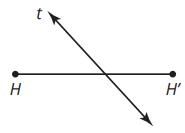
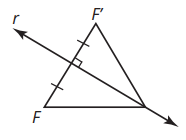
2nd example because it shows the points F and F' are equidistant from line r and that they are perpendicular to line r as well.
500
How many lines of symmetry does a circle have?
infinite
500
Which transformations happened?
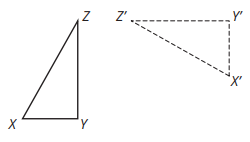
Rotate CCW 90 degrees and moves from ZZ'
500
Reflect across the y axis and up 3. Find Points A' and B'.
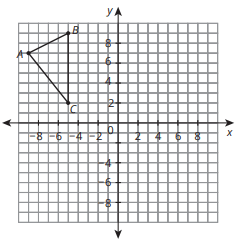
A'(9,10) and B'(5,12)
500
Triangle MATH = Triangle EVIL
Create a Triangle Congruency statements for Segments.
MA=EV
AT=VI
TH=IL
MH=EL