Composing Functions -- Values
Composing Functions -- Equations
Transformation Notation
100
If g(x) = x + 2, what is g(3)?
g(3)
means we should substitute 3 into the equation, so
g(3) = 3 + 2 = 5
100
If A(x)=x+1 and B(x)=x^2, find the expression for A(B(x))
A(B(x)) means we should substitute B(x) into A(x).
So instead of x + 1, we will have (x^2)+1, or just x^2 + 1
100
What transformation is represented by the notation f(x)-7?
A translation 7 units down
200
If g(x) = x + 2, what is g(g(3))?
g(g(3)) means we should substitute 3 into the equation and then substitute that value in again. Since g(3) = 5, then
g(g(3)) = g(5) = 5 + 2 = 7
200
If A(x)=x+1 and B(x)=x^2, find the expression for B(A(x))
B(A(x)) means we should substitute A(x) into B(x).
So instead of x^2, we will have (x+1)^2
200
What transformation is represented by the notation f(-x)?
A reflection over the y-axis, because the x value is changing signs
300
Below is the graph of a function R. What is R(R(0))?
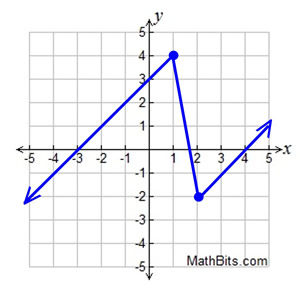
Since R(0) = 3,
R(R(0)) = R(3) = -1
300
If P(x)=sqrt(x) and Q(x)=x-3, find the expression for P(Q(x))
P(Q(x)) means we should substitute Q(x) into P(x).
So instead of sqrt(x), we will have sqrt(x-3)
300
What is the function notation that represents a translation 6 units to the right?
f(x-6)
400
If f(x) = 3x-1 and g(x)=x^2, what is f(g(2))?
f(g(2)) means we should do g(2) first.
g(2) = 2^2 = 4, so f(g(2))=f(4)=3(4)-1=11
400
If P(x)=sqrt(x) and Q(x)=x-3, find the expression for Q(P(x))
Q(P(x)) means we should substitute P(x) into Q(x).
So instead of x-3, we will have sqrt(x)-3
400
What is the function notation that represents scaling a function vertically by a factor of 5?
(Making the graph 5 times taller)
5f(x)
500
If w(x)=12-x and v(x) is shown in the graph below, find w(v(4))
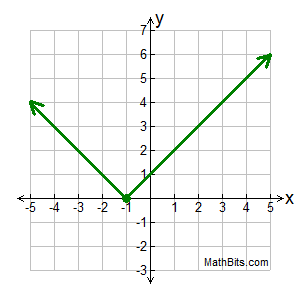
On the graph, we can see that v(4)=5
So w(v(4))=w(5)=12-5=7
500
If N(x)=(-2)/x and M(x)=x^2+10, find the expression for N(M(x))
N(M(x)) means we should substitute M(x) into N(x).
So instead of (-2)/x, we will have (-2)/(x^2+10)
500
Write any function notation that represents making a graph wider (horizontally stretching). The scale factor is your choice.
There should be a number between 0 and 1 multiplying x inside the parentheses.
For example, f(1/2x) or f(3/4x)