Factor and Solve Quadratics
System of Equations and Inequalities
Transformations of Figures
Standard vs Vertex Form
Square Roots
100
Factor the expression completely (hint: think GCF):
2x^2-18
2x(x-9)
100
Name the solution(s) of this system of equations.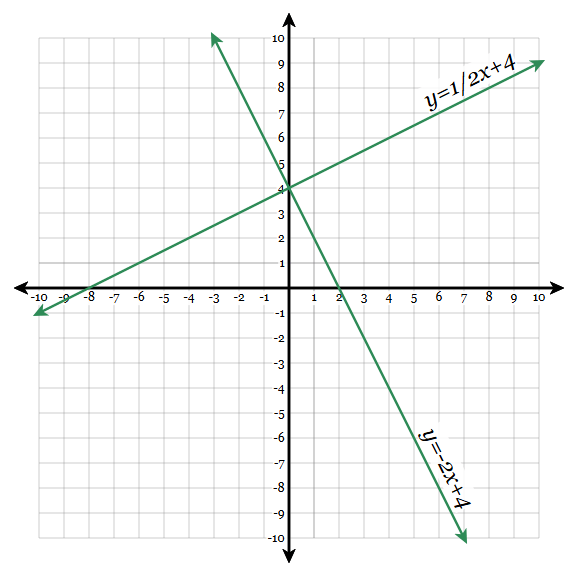
(0,4)
100
Name the four types of transformations.
Translation, Reflection, Rotation, Dilation
100
Determine the vertex of the graph.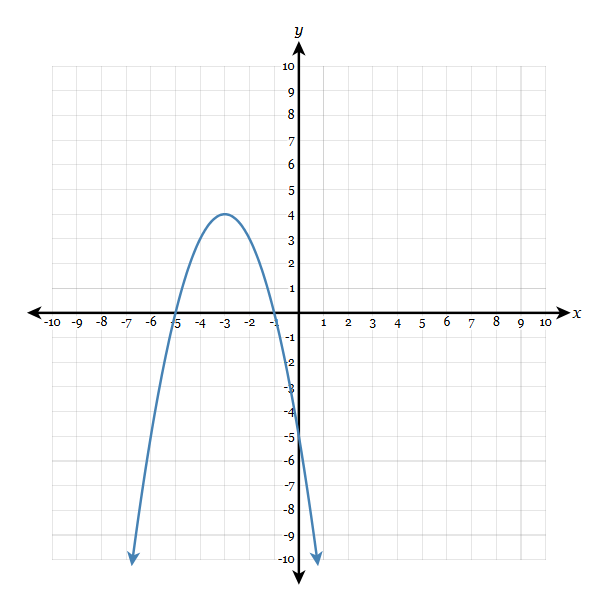
(-3,4)
100
Simplify the square root:
sqrt(80)
4sqrt(5)
200
Factor completely:
3x^2+4x+1
(3x+1)(x+1)
200
Name the solution(s) for the system of equations: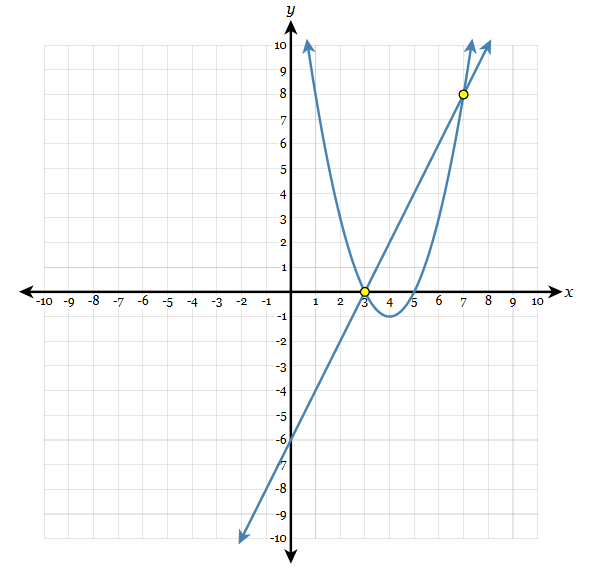 
(3,0) and (7,8)
200
What is the image point of (−6,5) after a translation right 2 units and down 4 units?
(-4,1)
200
What is the vertex of the quadratic equation?
y=(x-2)^2-5
(2,-5)
200
Determine the transformations from the parent function of
y=sqrt(x-6)+4
Right 6 and up 4
300
Solve Using the Quadratic Formula (keep your answer as a simplified radical):
2x^2+3x-4=0
(-3+-sqrt(41))/4
300
Find the solution(s) of the system of equations (write your answer as an ordered pair).
y=-2x and y=-6x+36
(9,-18)
300
Reflect the point (3,1) over the y-axis.
(-3,1)
300
Write the following equation in standard form (hint y=ax^2+bx+c):
y=(x-5)^2-32
y=x^2-10x-7
300
Solve:
sqrt(x+51)-18=-11
x=-2
400
Find the new constant c that would complete the square (hint: use the formula):
x^2-16x=13
64
400
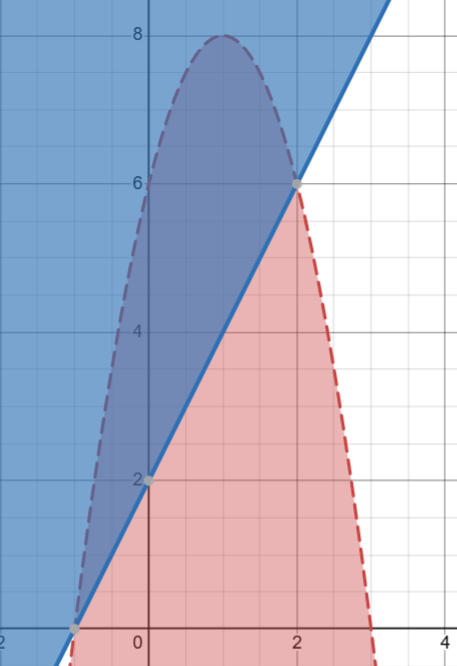
Name a coordinate point that exists in the system of inequalities:
y<-2x^2+4x+6 and y>=2x+2
400
Rotate (1,-3) 90 degrees counterclockwise.
(3,1)
400
Find the vertex of the quadratic equation (hint: use the formula to find x):
y=x^2+2x+19
(-1,18)
400
Solve:
sqrt(x+12)=x+6
x=-3
500
Solve Using the Quadratic Formula (keep your answer as a simplified radical):
2x^2-10x+5=-4
(5+-sqrt(7))/2
500
Name the solution(s) of the system of equations (write your answers as an ordered pair):
y=x^2-4x-44 and y=x+6
(10,16) and (-5,1)
500
Rotate the point (6,-3) 90 degrees clockwise then translate the point up 7.
(-3,1)
500
Convert the following quadratic equation to Vertex Form:
y=9x^2+18x+16
y=9(x+1)^2+7
500
Solve the quadratic equation by taking square roots (leave your answer as a simplified radical):
2+x^2=-9
x=+-isqrt(11)