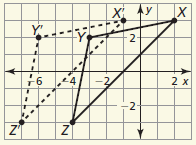
Translate △XYZ with vertices X(2, 3), Y(−3, 2), and Z(−4, −3) by (x, y) → (x, y + 2)
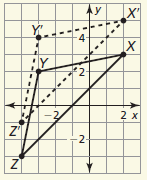
X'(2, 5), Y'(−3, 4), and Z'(−4, −1)
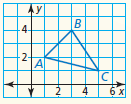
△ABC has vertices A(1, 3), B(4, 1), and C(1, 1).
Graph △ABC and its image after a reflection over the line y = x.
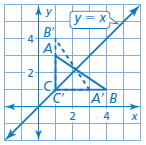
A'(3,1), B'(1,4), and C'(1, 1)
Graph the polygon with the given vertices and its image after a rotation of the given number of degrees about the origin.
A(−3, −1), B(2, 2), C(3, −3); 90°
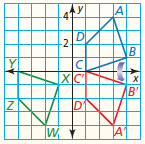
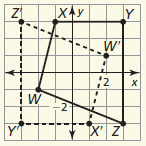
Describe a congruence transformation that maps quadrilateral ABCD to quadrilateral WXYZ.
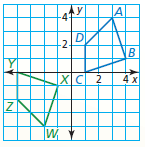
A congruence transformation that maps quadrilateral ABCD to quadrilateral WXYZ is a reflection in the x-axis followed by a translation of 5 units left.
Find the scale factor of the dilation. Then tell whether it is a reduction or an enlargement.
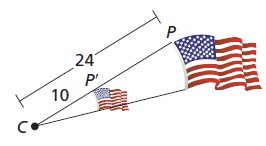
k = 5/12, reduction
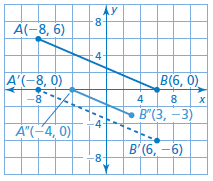
Line AB has endpoints A(−8, 6) and B(6, 0). Find the endpoints of its image after the similarity transformation.
Translation: (x, y) → (x, y − 6)
Dilation: (x, y) → (1/2x, 1/2y)
Translate △XYZ with vertices X(2, 3), Y(−3, 2), and Z(−4, −3) by (x, y) → (x − 3, y)
X'(-1, 3), Y'(−6, 2), and Z'(−7, −3)
How many lines of symmetry does the figure have?

1
Graph the polygon with the given vertices and its image after a rotation of the given number of degrees about the origin.
W(−2, −1), X(−1, 3), Y(3, 3), Z(3, −3); 180°
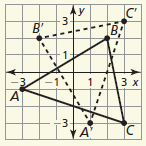
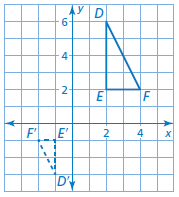
Describe a congruence transformation that maps △DEF to △JKL.
D(2, −1), E(4, 1), F(1, 2)
J(−2, −4), K(−4, −2), L(−1, −1)
reflection in the y-axis followed by a translation
3 units down
Graph △DEF with vertices D(2, 6), E(2, 2), and F(4, 2) and its image after a dilation with scale factor -1/2
Describe a similarity transformation that maps quadrilateral STUV to quadrilateral DEFG.
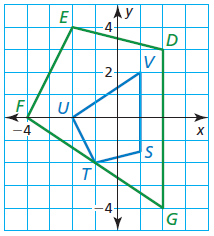
A reflection in the x-axis followed by a dilation with a scale factor of 2
Translate △XYZ with vertices X(2, 3), Y(−3, 2), and Z(−4, −3) by (x, y) → (x + 3, y − 1)
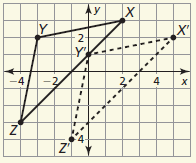
X'(5, 2), Y'(0, 1), and Z'(−1, −4)
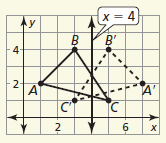
Graph the polygon and its image after a reflection over the given line, x=4.

Describe a congruence transformation that maps △DEF to △JKL.
D(−3, −4), E(−5, −1), F(−1, 1)
J(1, 4), K(−1, 1), L(3, −1)
180° rotation about the origin followed by a reflection in the line x = 2
Graph the triangle and its image after a dilation with scale factor k.
P(2, 2), Q(4, 4), R(8, 2); k = 1/2
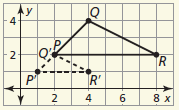
Describe a similarity transformation that maps △ABC to △RST.
A(1, 0), B(−2, −1), C(-1, -2)
R(-3, 0), S(6, -3), T(3, −6)
reflection in the line x = −1 followed by a dilation with center (−3, 0) and k = 3
Translate △XYZ with vertices X(2, 3), Y(−3, 2), and Z(−4, −3) by (x, y) → (x + 4, y + 1)
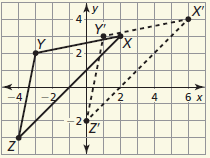
X'(6, 4), Y'(1, 3), and Z'(0, −2)
Graph the polygon and its image after a reflection in the given line, y=3.
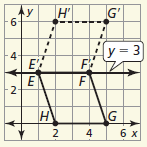
Determine whether the figure has rotational symmetry. If so, describe any rotations that map the figure onto itself.

yes; Rotations of 60°, 120°, and 180° about the center map the figure onto itself.
Which transformation is the same as reflecting an object in two parallel lines?
translation
Graph the triangle and its image after a dilation with scale factor k.
X(−3, 2), Y(2, 3), Z(1, −1); k = −3
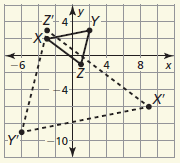
Describe a similarity transformation that maps △ABC to △RST.
A(6, 4), B(−2, 0), C(−4, 2)
R(2, 3), S(0, −1), T(1, −2)
dilation with center at the origin and k = 1/2, followed by a reflection in the line y = x
What are the vertices of △P"Q"R" with vertices P(0, −4), Q(1, 3), and R(2, −5) after the composition
Translation: (x, y) → (x + 1, y + 2)
Translation: (x, y) → (x − 4, y + 1)
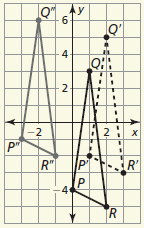
P'(1, −2), Q'(2, 5), and R'(3, −3)
P''(-3, −1), Q''(-2, 6), and R''(-1, −2)
How many lines of symmetry does the figure have?
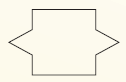
2
Determine whether the figure has rotational symmetry. If so, describe any rotations that map the figure onto itself.
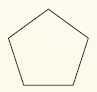
yes; Rotations of 72° and 144° about the center map the figure onto itself.
Which transformation is the same as reflecting an object in two intersecting lines?
rotation
You are using a magnifying glass that shows the image of an object that is eight times the object’s actual size. The image length is 15.2 centimeters. Find the actual length of the object.
1.9 cm
Describe a similarity transformation that maps △ABC to △RST.
A(3, −2), B(0, 4), C(−1, −3)
R(−4, −6), S(8, 0), T(−6, 2)
270° rotation about the origin followed by a dilation with center at the origin and k = 2