Rotations
Reflections
Translations
Dilations
Similar or Congruent?
100
Describe the rotation shown that takes the orange triangle onto the green triangle.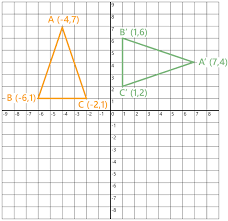
90 degree rotation about the origin.
100
Write the coordinate rule for a reflection over the x-axis.
(x, y) --> (x, -y)
100
Describe the translation that takes the blue triangle onto the red triangle in words.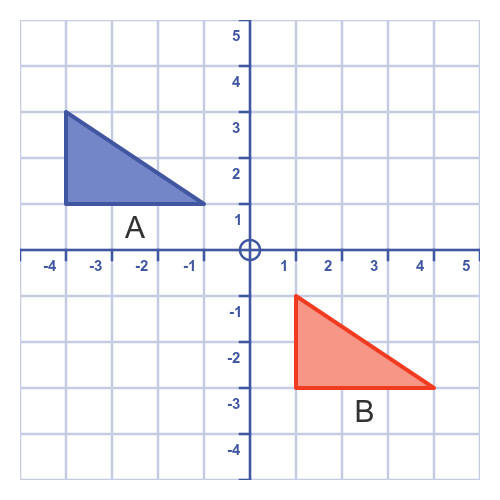
Translate right 5 and down 4.
100
Dilations create __________ figures. (Similar or congruent?)
Similar
100
Which transformations can create congruent figures? Name each one.
Rotations, Reflections, and Translations
200
Describe the rotations shown that takes the red triangle onto the blue triangle.
180 degree rotation about the origin.
200
Describe the reflection that takes the blue triangle onto the red triangle.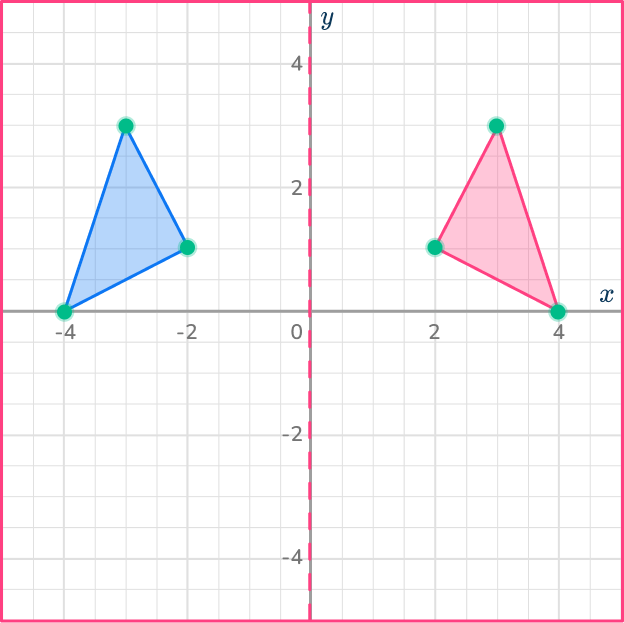
Reflection over the y-axis.
200
Describe the translation that takes the blue triangle onto the red triangle in words.
Translate left 6 and up 2.
200
Determine the scale factor for the dilation that takes the blue triangle onto the orange triangle.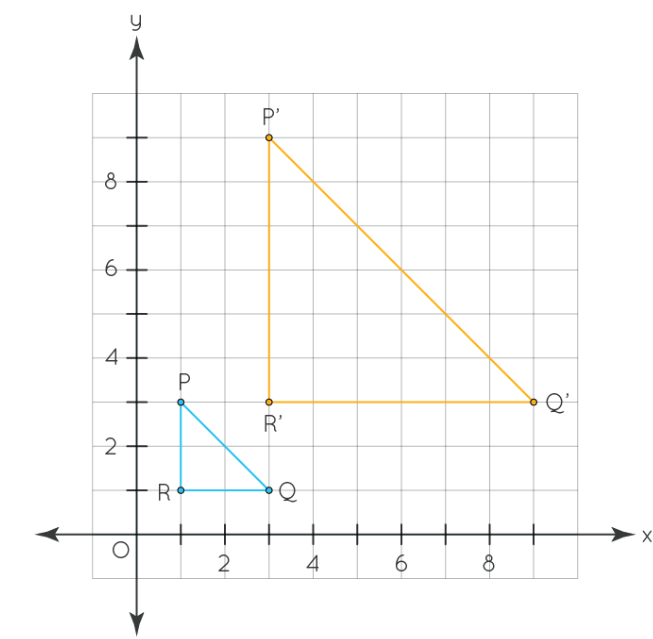
3
200
A triangle is rotated 90 degrees clockwise about the origin, reflected over the y-axis, then translated down 2 units. Is the resulting triangle similar or congruent to the original triangle? Explain how you know.
Yes, those transformations are rigid transformations that do not change the size or shape of an object.
300
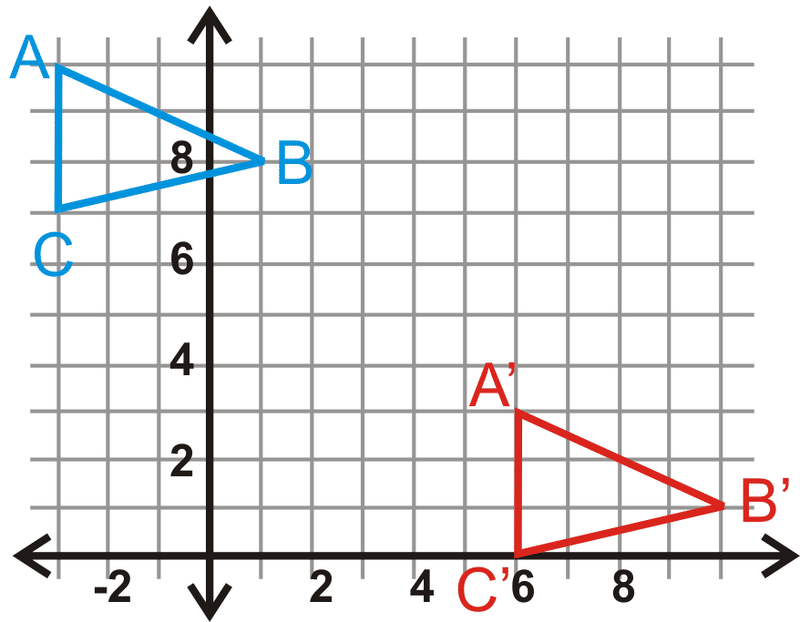
Describe the rotation that takes triangle ABC onto the red triangle.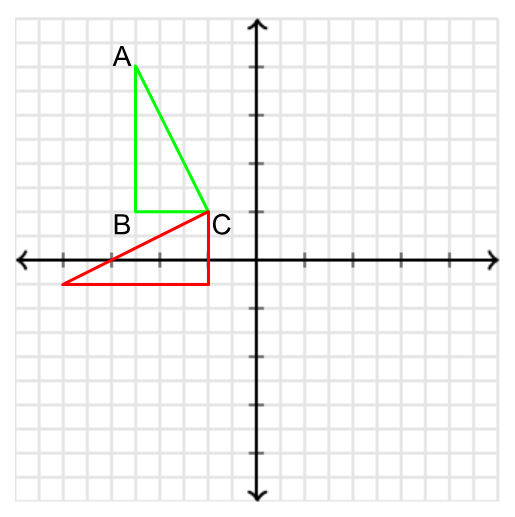
90 degree counterclockwise rotation about C.
300
Describe the reflection that takes triangle ABC onto triangle DEF.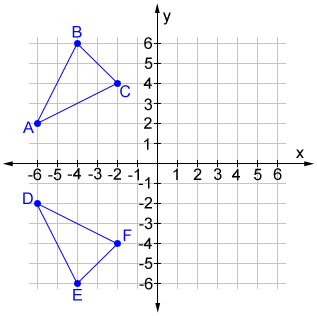
Reflection over the x-axis.
300
Write the coordinate rule that describe the translation shown.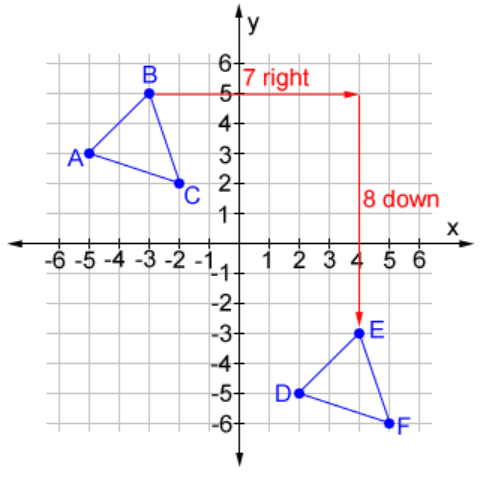
(x, y) --> (x + 7, y - 8)
300
Which scale factor could take the grey triangle onto the green triangle.
(a) 2.5 (b) -2 (c) 0.5 (d) -0.5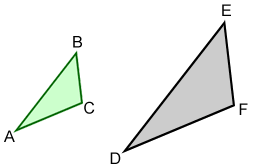
(c) 0.5
300
A rectangle is dilated by a scale factor of 1.5, reflected over the y-axis, then rotated 90 degrees clockwise. Is the resulting triangle similar or congruent to the original triangle? Explain how you know.
Similar, a dilation occurred which changed the triangle's size.
400
Describe the rotation that takes the red parallelogram onto the green parallelogram.
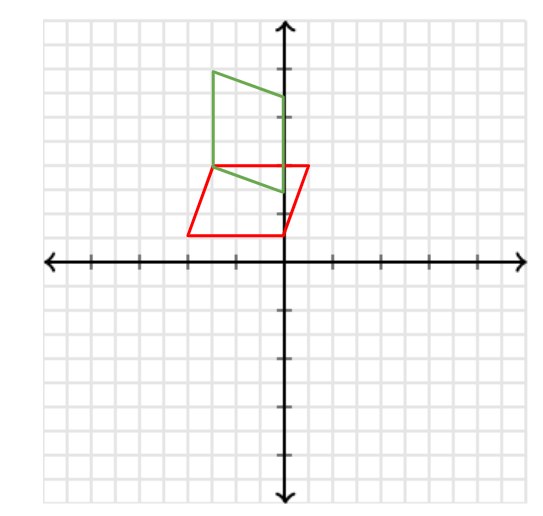
90 degree rotation counter clockwise about the point (-3, 4).
400
Describe how to take the orange triangle onto the pink triangle using reflections.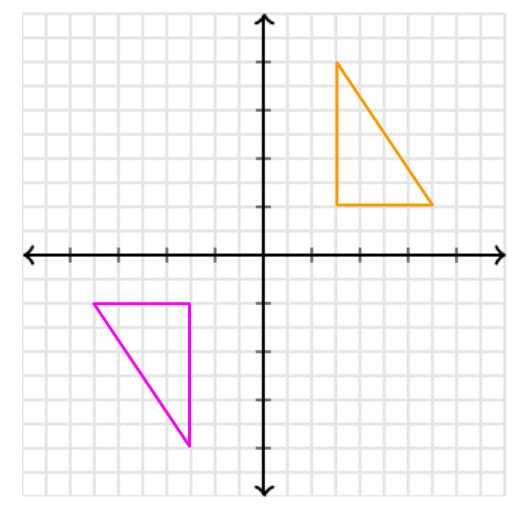
Reflect over the x-axis, then reflect over the y-axis.
Reflect over the y-axis, then reflect over the x-axis.
400
Write the coordinate rule for the translation that takes the blue triangle onto the red triangle.
(x, y) --> (x + 8, y - 7)
400
True or false: All sides and angles are multiplied by the scale factor during a dilation.
False, angles do not change.
400
Are the triangles shown similar? If so, what is the scale factor?
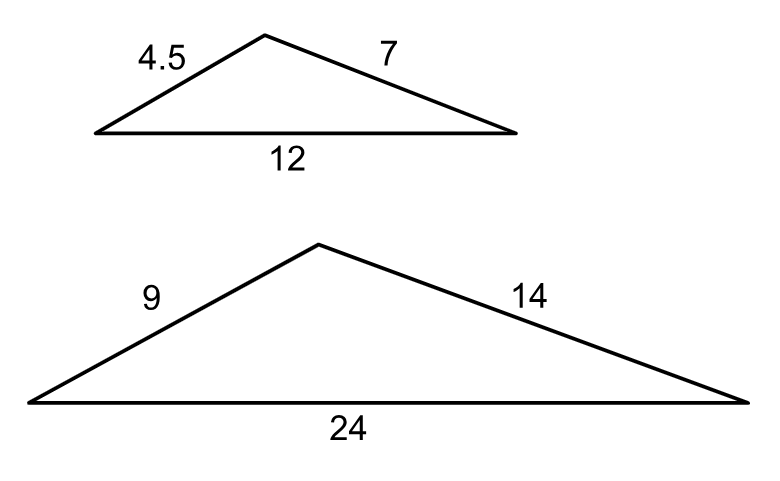
Yes, the scale factor is either 2 or 0.5.
500
Describe the rotation that takes the blue trapezoid onto the orange trapezoid.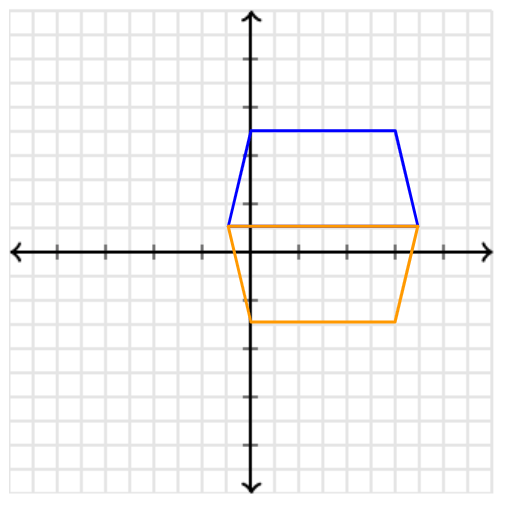
180 degree rotation about the point (3, 1)
500
What single transformation is equivalent to a reflection over the x-axis followed by a reflection over the y-axis?
180 degree rotation about the origin.
500
Write a coordinate rule for a translation down 9 units.
(x, y) --> (x, y - 9)
500
Determine the scale factor that would map quadrilateral A onto quadrilateral B.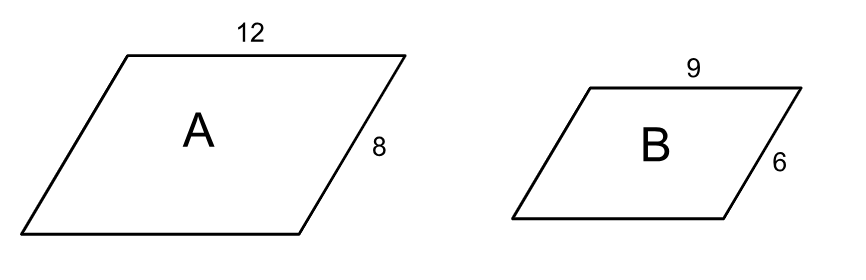
3/4 or 0.75
500
Are the shapes shown similar? If so what is the scale factor?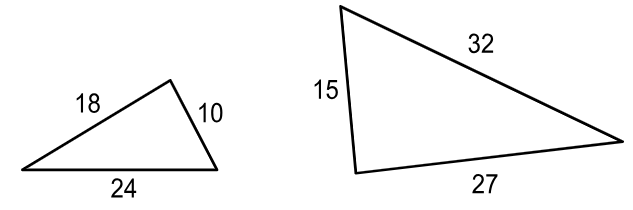
No