OR
the x-coordinate is the opposite
What is (x,y) → (-x,-y)?
Side Length
Angle Measure
Orientation

List All Congruent Parts.
Angle ABC and Angle DEF
Angle BCA and Angle EFD
Angle CAB and Angle FDE
Side AB and Side DE
Side BC and Side EF
Side AC and Side DF
Which parts are congruent?
Angle BCA and Angle YZX
Angle CAB and Angle ZXY
Side AB and Side XY
Side AC and Side XZ
Side BC and Side YZ
Which single translation will produce the same image as the following sequence of translations:
(x, y) → (x - 1, y + 5), followed by
(x, y) → (x + 4, y + 2), followed by
(x, y) → (x - 5, y - 7)
(x,y)→ (x-2,y) OR
Translate left 2 units

Which parts of these triangles are congruent?
Angle ABC and Angle DEF
Angle BCA and Angle EFD
Angle CAB and Angle FDE
Side AB and Side DE
Side BC and Side EF
Side AC and Side DF
X(0,3)→(0-5,3+1)→X'(-5,4)
Y(3,-2)→(3-5,-2+1)→Y'(-2, -1),
Z(4,0)→(4-5,0+1)→Z'(-1, 1)
OR
the y-coordinate is opposite
What is (x, y)→(y, -x)?
Translate down 1, rotate 90 degrees counterclockwise, then reflect over the y-axis.

When we complete a transformation on a set of parallel lines, what is one way that we can tell that the lines are still parallel other than the slope?
If triangle ABC has coordinates A(-2, 0), B(1, 3), and C(3, -4), what are the new coordinates when reflected over the x-axis?
Find the coordinates of A' and B' when A(-3, -2) and B(-1, 2) are rotated clockwise 180 degrees around the origin.
(x,y)→(-x,-y)
A(-3,-2)→A'(3,2)
B(-1,2)→B'(1, -2)?
Rotate L 90 degrees counterclockwise around the origin.
Reflect L' over the y-axis,
then translate L'' two units down and three units to the right.
What is your new coordinate?
(3,-2)→(2,3)
(2,3)→(-2,3)
(-2,3)→(-2+3,3-2)→(1,1)
A 90 degree rotation is shown. Is Orientation preserved? Why/Why Not?
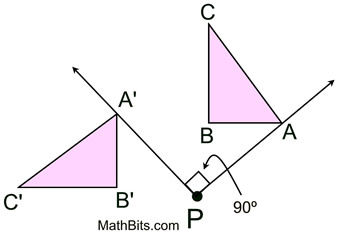
Yes, if we start at A:
A→B→C
A'→B'→C'
X and Y-Values were switched.
Rotate Triangle RST 90 degrees clockwise if Triangle RST has coordinates R(2,4), S(3,-2), and T(-6,12)
(x,y)→(y,-x)
R(2,4)→R'(4,-2)
S(3,-2)→S'(-2,-3)
T(-6,12)→T'(12,6)
Point A is mapped to point A' (-1,4) after a translation of up 4 and left 3, then a reflection over the x-axis.
What is the original point of A?
Backwards Order
(-1,4) -> (-1,-4)(-1,-4) -> (-1+3, -4-4) -> (2,-8)
 What is a reflection?
What is a reflection?