Vocabulary
Translations
Reflection
Rotation
Congruency
100
What is a rigid transformation?
A transformation that preserves size & shape.
100
A square with side length 2 units is translated 5 units up. What happens to its area?
The area remains the same.
100
The given graph depicts a rigid transformation.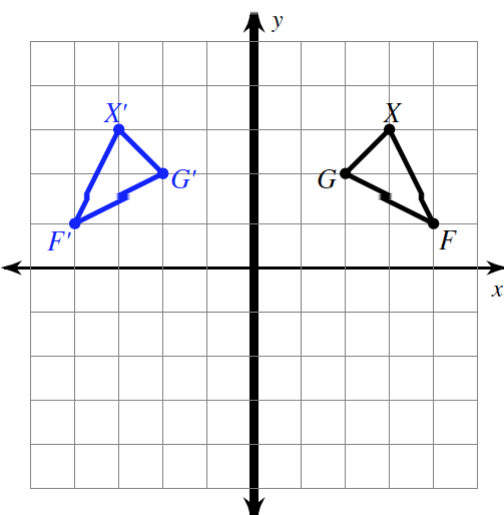
What is a reflection in the y-axis?
100
The given graph depicts a rigid transformation.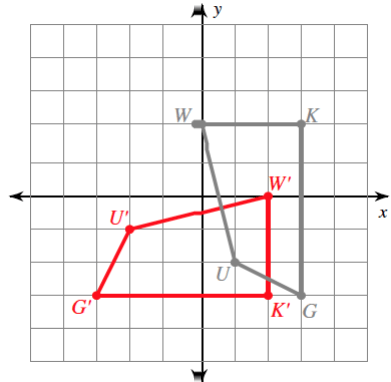
What is a 90-degree clockwise rotation?
100
What does it mean for two figures to be congruent?
Same shape and size.
200
Name the three types of rigid transformations.
Translation, reflection, rotation.
200
Translate point A(–2, 4) by the rule (x, y) →
(x + 3, y – 2). What is A′?
(1, 2)
200
The figure has been reflected over this line.
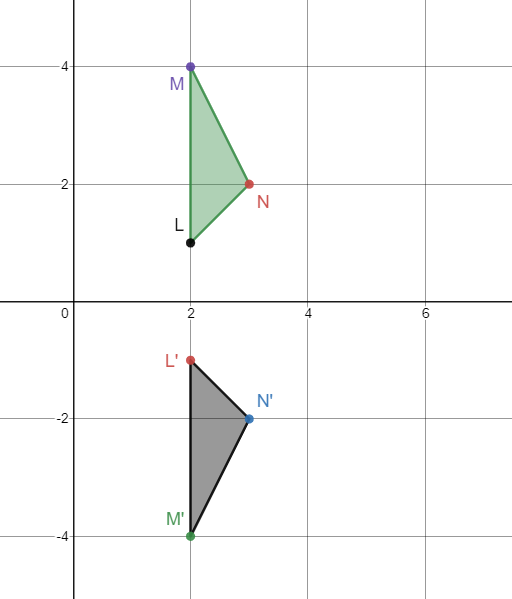
What is the x-axis?
200
A square is rotated 90° counterclockwise, then translated up 3 units. How is its size affected?
Size unchanged.
200
True or False: If two figures can be mapped onto each other using rigid transformations, they are congruent.
True.
300
Define congruent figures
Figures with same shape & size.
300
Write a Sequence of transformations that moves point P(–5, 0) to P′(2, 7).
(x + 7, y + 7)
300
Reflect point (4, –2) across the y-axis. What is the new point?
(–4, –2)
300
The given graph depicts rigid transformations of the pre-image *. This triangle represents a Rotations of * 90-degrees counterclockwise about the origin.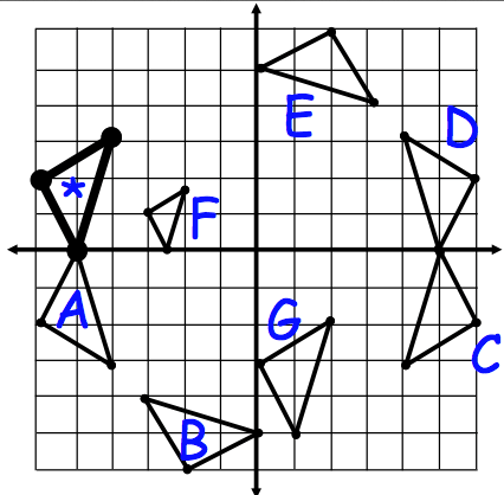 
What is figure B?
300
A triangle has vertices at (0,0), (2,0), (1,3). Another triangle has vertices (–2,0), (0,0), (–1,3). Describe the transformation(s) that prove the triangles are congruent.
Reflection across y-axis.
400
True or False: Dilations are rigid transformations.
False, surprise that is your next unit;)
400
Translate triangle with vertices (1,1), (2,3), (3,1) 4 units right. List new coordinates.
(5,1), (6,3), (7,1)
400
A triangle at (1,2), (2,4), (3,2) is reflected over the y-axis and then translated 1 unit down. Write its new coordinates.
(–1,1), (–2,3), (–3,1)
400
Rotate point (0, 5) 180° about the origin. What is the new point?
(0, –5)
400
Two triangles are congruent. One has sides 3, 4, 5. What are the side lengths of the other triangle?
3, 4, 5.
500
Explain the difference between a rigid transformation and a non-rigid transformation.
Rigid = preserves size; non-rigid (dilation) = changes size.
500
A figure is translated left 2 and up 3. Describe this movement using a coordinate rule.
(x – 2, y + 3)
500
Reflect triangle with vertices (1,1), (2,2), (3,1) across the x-axis. List new coordinates.
(1, –1), (2, –2), (3, –1)
500
Rotate point (–3, 2) 90° clockwise about the origin.
(2, 3)
500
Explain why all rigid transformations preserve congruence. Give an example using coordinates.
They preserve distance and angle measures