Unit 1 pt.1
Unit 1 pt.2
Unit 2 pt.1
Unit 2 pt.2
Unit 3 pt.1
Unit 3 pt.2
Unit 8
100
Is this symmetric to the y-axis, x-axis, origin, or neither?
y = x4 +x - 3
Niether
100
Find the distance between the points :
(-1,8) and (4,-2)
5sqrt(5)
100
Either use long or synthetic division to divide
(-20x2 +6x4 -16) / (2x+4)
3x3 -6x2 +2x -4
100
Solve the inequality
5y2 + 7y < 3(y + 4)
(-2, 6/5)
100
Graph
f(x) = 2^x+3
" Find the domain, range, asymptote"
"Domain : " (-oo, oo)
"Range : " (3,oo)
"Asymptote : " y = 3
100
Given
h(x) = (x-7)/4 ", find " h^-1(x)
h^-1(x) = 4x + 7
100
Stuart pays back two student loans over a 4-yr period. One loan charges the equivalent of 3% simple interest and the other charges the equivalent of 5.5% simple interest. If the total amount borrowed was $32,000 and the total amount of interest paid after 4 yr is $4640, find the amount borrowed from each loan.
24,000 at 3%
8,000 at 5.5%
200
Can you graph:
f(x) = -(x-1)^2-2
Check desmos
200
Find difference quotient:
(f(x+h) - f(x) ) / h
f(x) = 3x2-4x+9
6x+3h-4
200
Find the vertex and write the expression in vertex form
f(x) = 3x2 -42x -91
(7,-238)
f(x) = 3(x-7)2 -238
200
After months of data collection, the sales team determines that the monthly profit is approximated by f(p) = -50p^2 + 1700p - 12,000, where p is the price per shirt and f(p) is the monthly profit based on that price.
a. Find the price that generates the maximum profit
b. Find the maximum profit
a. $17
b. $2450
200
Determine if the function is one-to-one:
f(x) = x^3-2x
Yes, it's one-to-one (passes horizontal line test).
200
Expand
log_3(6xy^2)
log_3(6)+log_3(x)+2log_3(y)
200
The average weekly salary of two employees is $1200. One makes $200 more than the other. Find their salaries.
One makes $1100 and the other makes $1300
300
Find the function and write the domain in interval notation:
n(x) = x^2-4x
p(x) = sqrt(x-2)
(n/p)(x)
"Domain: " (2, oo)
300
Graph the piecewise function:
|x| for x <= 2
2 for x > 2
Increasing, decreasing, constant intervals?
Check on desmos
"Decreasing" (-oo, 0)
Increasing (0,2)
"Constant" (2, oo)
300
Determine y intercept, x intercept, vertical asymptotes, horizontal asymptotes and slant asymptote
h(x) = (2x^2 + 9x + 4) / (x + 3)
y int : (0, 4/3)
x int : (-1/2, 0) and (-4, 0)
VA: x = -3
Slant asymptote : y = 2x + 3
300
Can you sketch this equation
f(x) = x3 -5x2
Hint: Think about multiplicities and zero product property
Check desmos
300
Polo borrows $5000 for 6 years, he has the option to do a simple interest at 6% or do a compounded continuously at 5.5%, which option would be greater?
"Simple = 1800"
"Continuous = 1882.07"
"Continuous would be greater"
300
A lab starts with a bacteria culture containing 500 bacteria. The population doubles every 3 hours.
"a) Write a function of the form " P(t) = P_0e^(kt) " to model the population P(t) after t hours"
"b) How many bacteria will there be after 9 hours?"
"c) After how many hours will the population reach 8000 bacteria? Round to the nearest tenth."
"a) " P(t) = 500e^(0.2310t)
"b) " 3996.5
"c) 12 hours"
300
Solve the system
-6x - 3y + 7z = -7
-x + 2y -7z = -10
-3x + 2y -8z = -16
(2,3,2)
400
A dance studio has a fixed monthly costs of $1500. The studio charges $60 for each private lesson, but has a variable cost for each lesson of $35 to pay the instructor.
What is the cost function?
What is the revenue function?
What is the profit function?
Determine the break-even point.
C(x) = 35x + 1500
R(x) = 60x
P(x) = 25x - 1500
Break even : x = 60
400
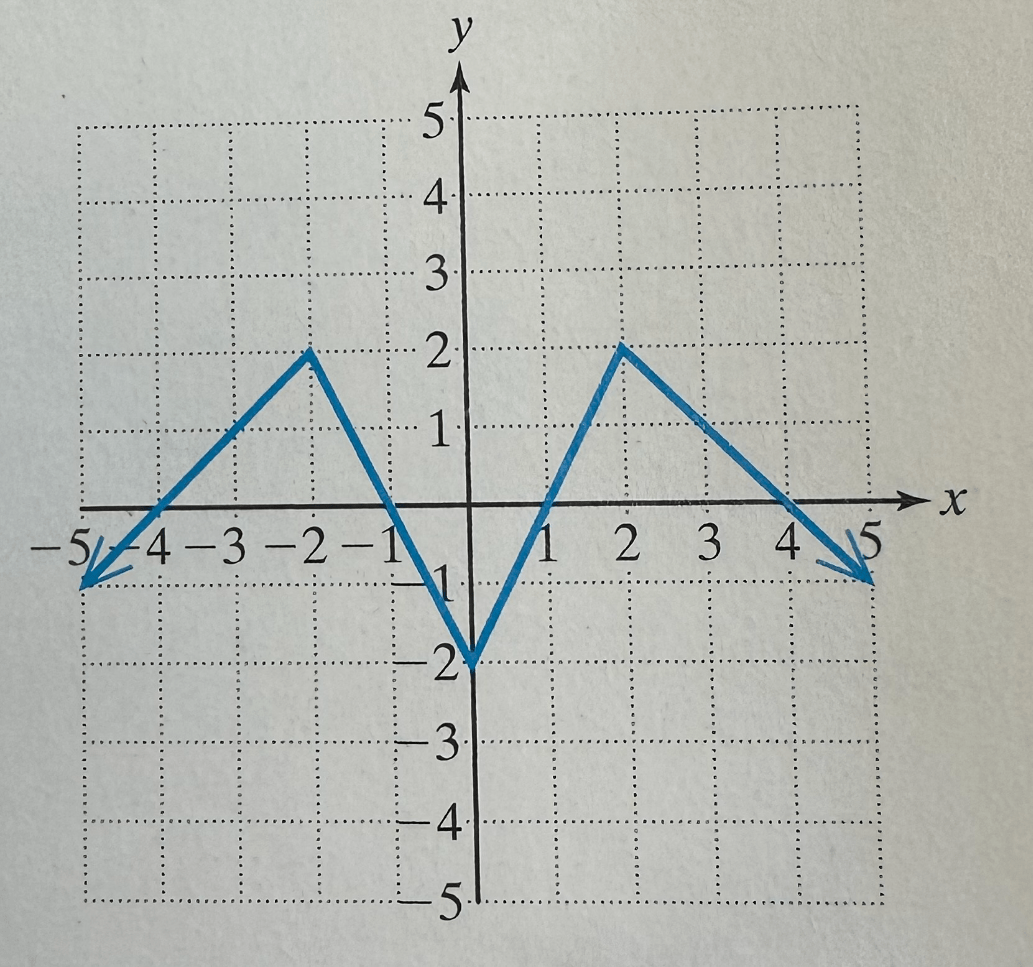
What location and value do we have relative min and relative max?
This is even, odd, or neither function?
At x = 0, the function has a relative min of -2
At x = -2, the function has a relative max of 2 and at x = 2, the function has a relative max of 2
Even Function
400
Find all zeros and factor f(x) as a product of linear factors
f(x) = x4 - 6x3 + 5x2 + 30x - 50 ; 3 - i is a zero
x = 3 - i, 3 + i, sqrt(5), - sqrt(5)
(x - (3 + i)) (x - (3 - i)) (x - sqrt(5)) (x + sqrt(5))
400
What is the horizontal asymptote of
(x4 +2x +1) / (5x+2)
No horizontal
400
Solve
log_4(x-1)+log_4(x+1)=1
x = +- sqrt5
400
Suppose that $18,000 is invested in a bond fund and the account grows to $23,344.75 in 5 yr
"Use the model " A=Pe^(rt) " to determine the average rate of return "
"under continuous compounding. Round to the nearest tenth of a percent."
r = 5.2%
400
Find the partial fraction decomposition
(-4x-2) / (x^2 + 2x)
-1/x+ -3/(x+2)