Common Reasons for Proofs
Congruence Statements
Random
Triangle Congruence
Triangle Congruence Postulates
100
What mark are we allowed to make on this figure?
AB=AB Both triangles share the same side.
100
Given this congruence statement, the angle congruent to angle V.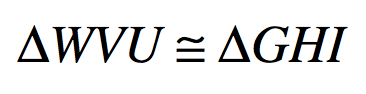
What is
angleH
100
What congruent parts information would we need to know for the triangles to be congruent by ASA?
EC = DC
100
The congruence conjecture that proves these are congruent triangles.
What is SSS?
100
By what method can you prove these two triangles are congruent (if any)?
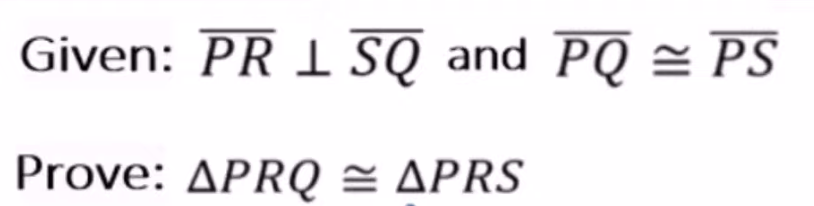
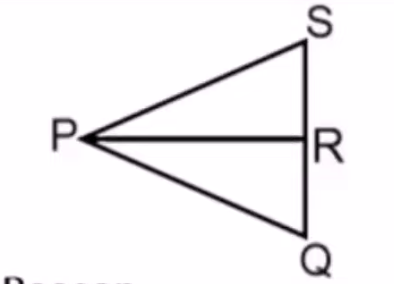
HL-Theorem
200
Given: C is the midpoint of AE.
What parts of the two triangles are now congruent?
AC=EC
200
The side congruent to side VU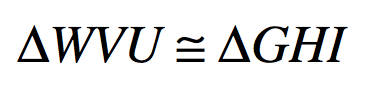
What is
bar{HI}
200
What congruent parts would make these triangles congruent by AAS?
AC = DE
OR
BC = FE
200
The congruence conjecture that proves these are congruent triangles.
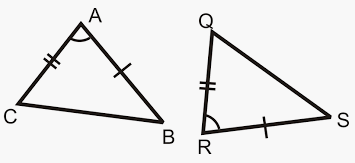
What is SAS?
200
By what method can you prove these two triangles are congruent (if any)?
Not congruent
300
Given:
bar{AE} text( bisects )bar{BD}
Name the parts we are allowed to mark congruent:
bar{BC} text( and )bar{CD}
300
A congruence statement for the two triangles represented by:
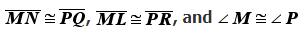
What is
triangleMNLcongtrianglePQR
300
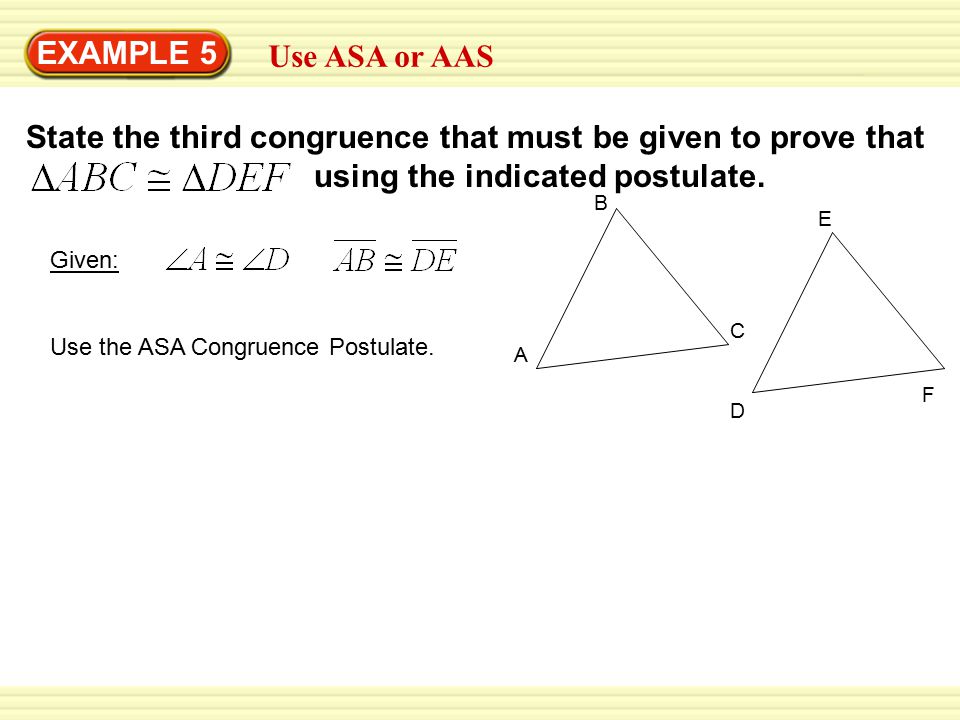
ASA if <B = <E
300
Are the following triangles congruent? If so, name the congruence conjecture that proves it.
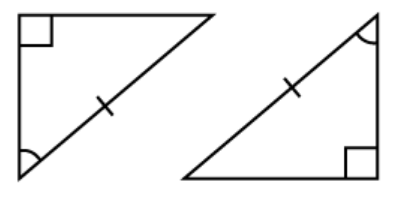
What is AAS?
300
By what method can you prove these two triangles are congruent (if any)?
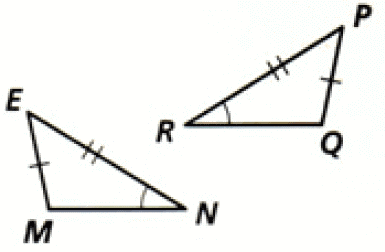
Not congruent
400
What is the reason we can mark this as true:
∠BCA ≅ ∠ECD
Vertical Angles
400
The side congruent to IG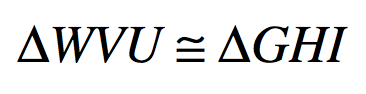
What is
bar{UW}
400
Solve for x and y
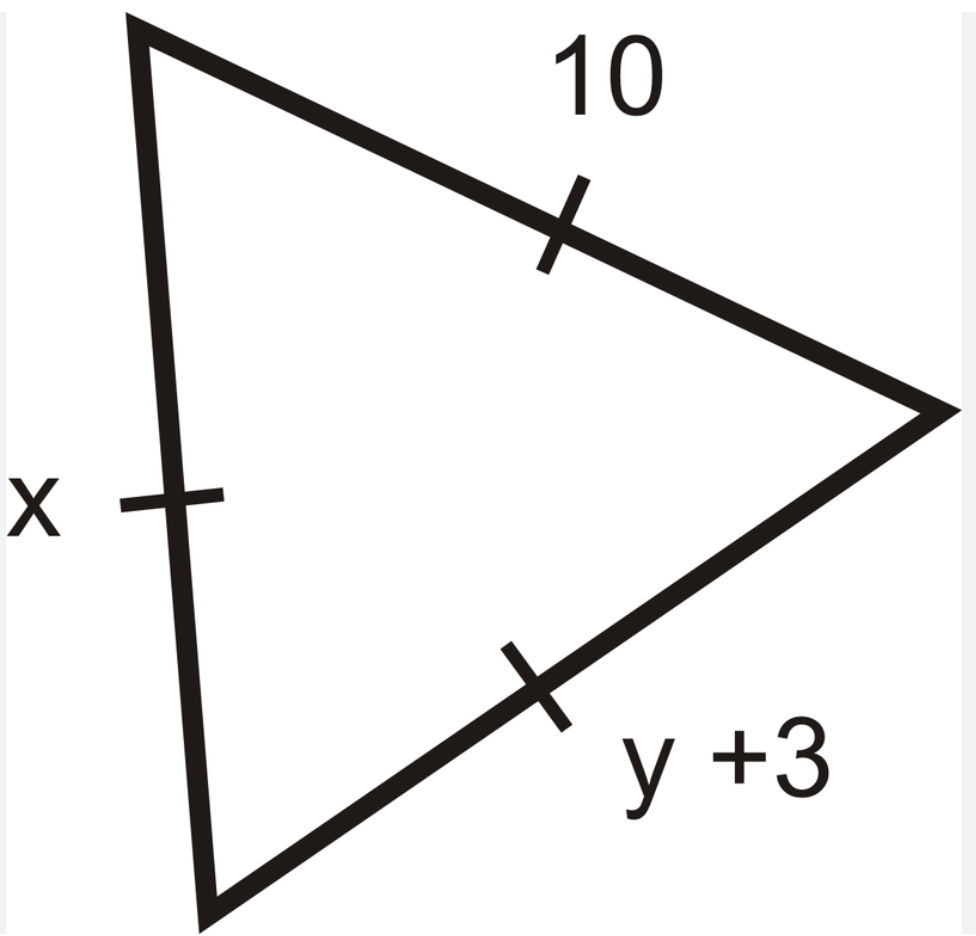
x=10
y=7
400
Are the following triangles congruent? If so, name the congruence conjecture that proves it.
What is SAS?
400
By what method can prove these two triangles are congruent (if any)?
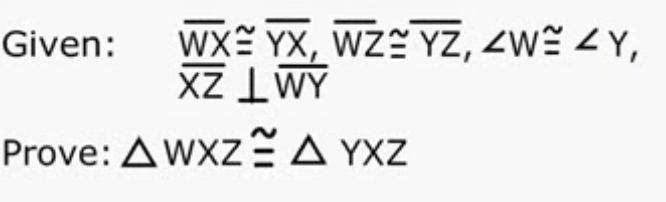
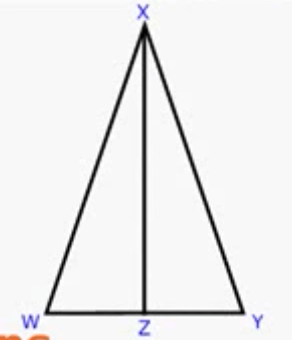
Answers may vary
ASA,AAS, SSS, HL, SAS
500
Given:
bar{BD} text( bisects )angle ABC
Statement: (What parts of the triangle are now congruent: )
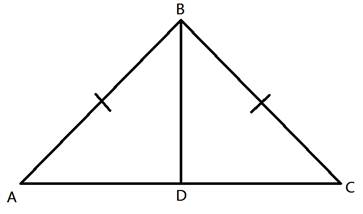
Statement:
angle ABD text( = )angle CBD
500
Congruence statement for the triangles represented by:
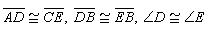
What is
triangleADBcongtriangleCEB
500
Solve for x?
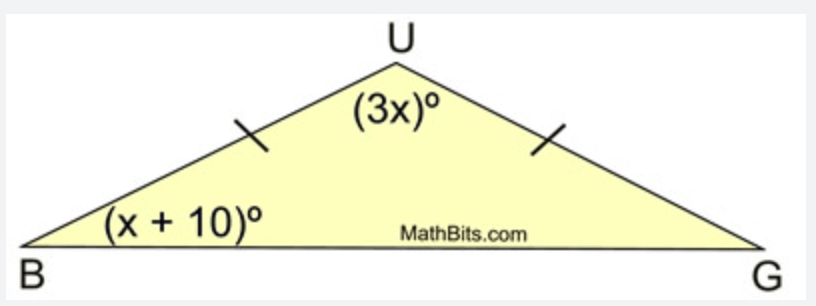
x=32
500
The additional information needed to prove the two triangles are congruent using HL theorem
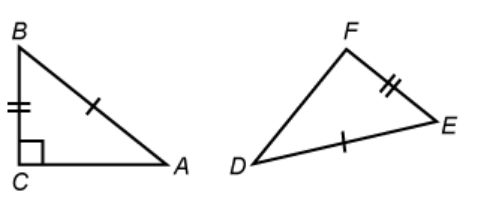
ANGLE F has to be equal to 90*
500
By what method can you prove these two triangles are congruent (if any)?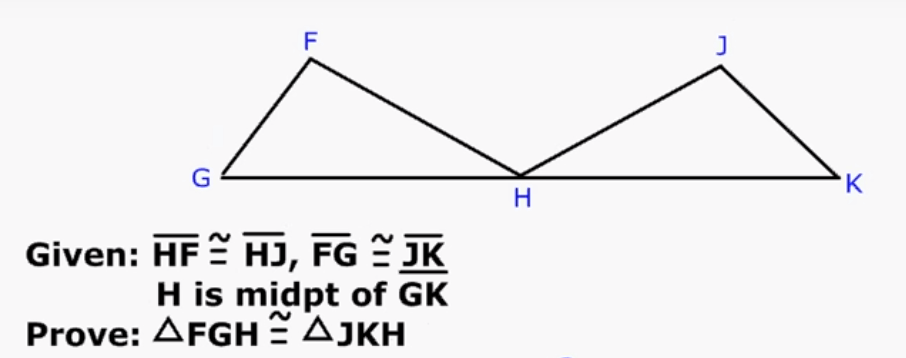
SSS