What is the name of the theorem that states that if two angles and the included side of one triangle are congruent to the corresponding angles and included side of another triangle, then the triangles are congruent?
ASA
What are the three properties of congruence for triangles?
The three properties of congruence for triangles are: angle congruence, side congruence, and CPCTC.
If two triangles are congruent, what can you conclude about their corresponding angles?
The corresponding angles of congruent triangles are congruent.
What does the term "congruent triangles" mean?
Congruent triangles have the same shape and size, with corresponding sides and angles that are equal.
Are these triangles congruent?
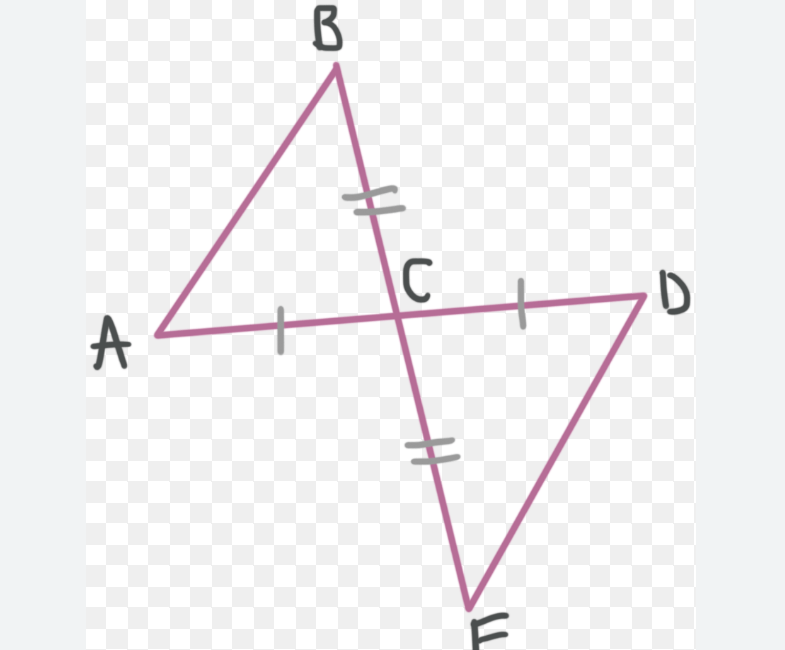
Yes
Which triangle congruence theorem states that if all three sides of one triangle are congruent to the corresponding sides of another triangle, then the triangles are congruent?
SSS
How many sides of a triangle need to be congruent to establish triangle congruence using the SAS property?
Two sides of a triangle need to be congruent to establish triangle congruence using the SAS property.
If two triangles are congruent, what can you conclude about their corresponding sides?
The corresponding sides of congruent triangles are congruent.
Name the four methods of proving triangle congruence.
SSS (Side-Side-Side), SAS (Side-Angle-Side), ASA (Angle-Side-Angle), and AAS (Angle-Angle-Side) are the four methods of proving triangle congruence
What rigid transformation maps triangle ABC onto triangle DEC? 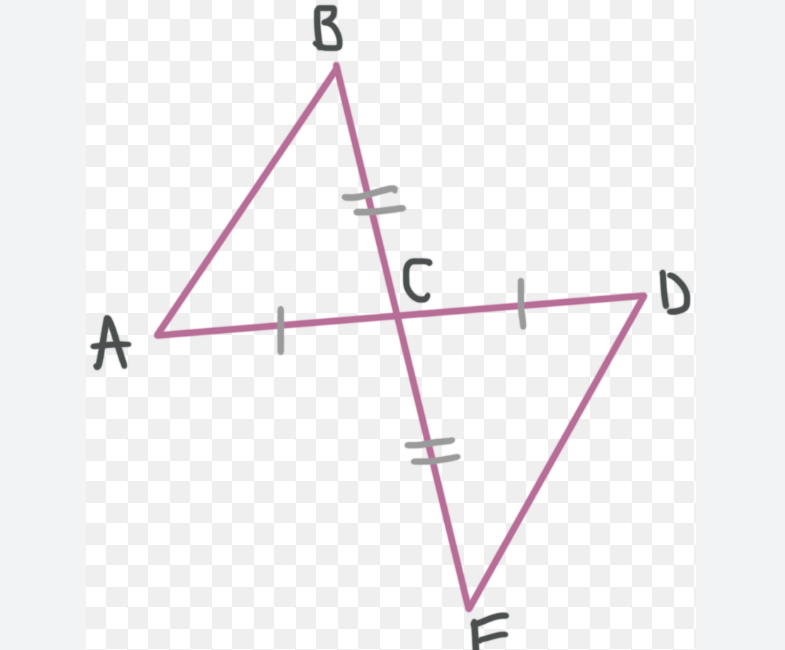
Rotation in either direction about center point C
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, which triangle congruence theorem can be used to prove the triangles congruent?
SAS
How many angles of a triangle need to be congruent to establish triangle congruence using the ASA property?
Two angles of a triangle need to be congruent to establish triangle congruence using the ASA property.
Name two postulates or theorems for proving triangle congruence.
SAS (Side-Angle-Side), ASA (Angle-Side-Angle), SSS (Side-Side-Side), AAS (Angle-Angle-Side), HL (Hypotenuse Leg)
Define the term "corresponding parts" in the context of triangle congruence.
Corresponding parts refer to the matching sides and angles of congruent triangles.
According to the image below.. What is congruent to line segment BC?
CE or EC
What is the name of the theorem that states if two angles and a non-included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, then the triangles are congruent?
AAS
If all three sides and all three angles of two triangles are congruent, what can we conclude about the triangles?
If all three sides and all three angles of two triangles are congruent, the triangles are congruent.
State the CPCTC (Corresponding Parts of Congruent Triangles are Congruent) theorem.
If two triangles are congruent, then their corresponding parts (angles and sides) are congruent.
or
If triangles are the same both triangles will have same side lengths and angles.
In triangle congruence, what are vertically opposite angles?
Vertically opposite angles are the angles formed by the intersection of two lines and are opposite each other. They have equal measures.
What is the angle relationship represented in this image?
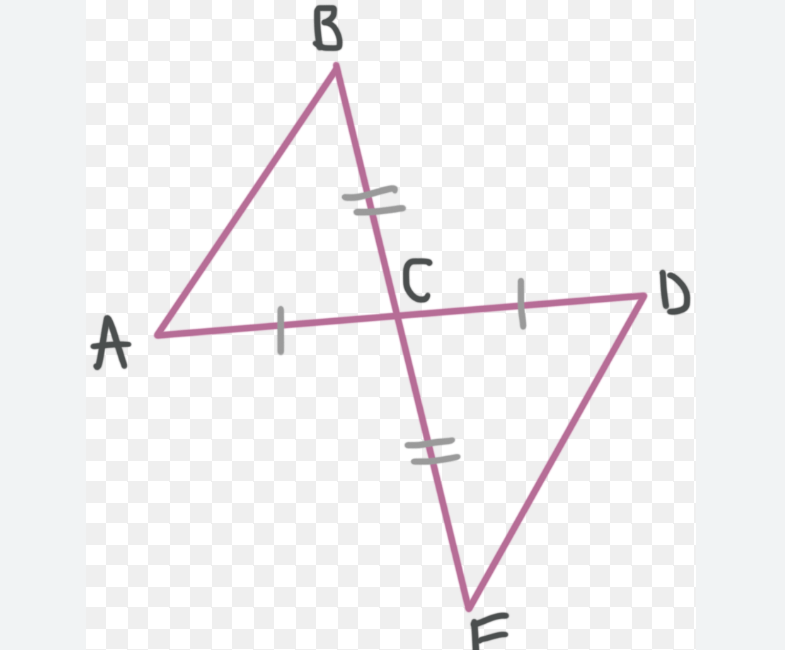
Vertical Angles
Which theorem is true when two right triangles are congruent due to the hypotenuses and one of their corresponding legs are being congruent? (Specific to right triangles)
HL
If two triangles have two pairs of corresponding congruent angles, what can we conclude about the triangles?
If two triangles have two pairs of corresponding congruent angles, the triangles are similar but not necessarily congruent.
Give an example of a postulate we have looked at that proved to be inconclusive on whether or not triangles are congruent
AS* .. SSA .. AAA
Explain what the Hypotenuse-Leg (HL) Congruence Theorem states.
The Hypotenuse-Leg (HL) Congruence Theorem states that if the hypotenuse and one leg of a right triangle are congruent to the hypotenuse and one leg of another right triangle, then the two triangles are congruent.
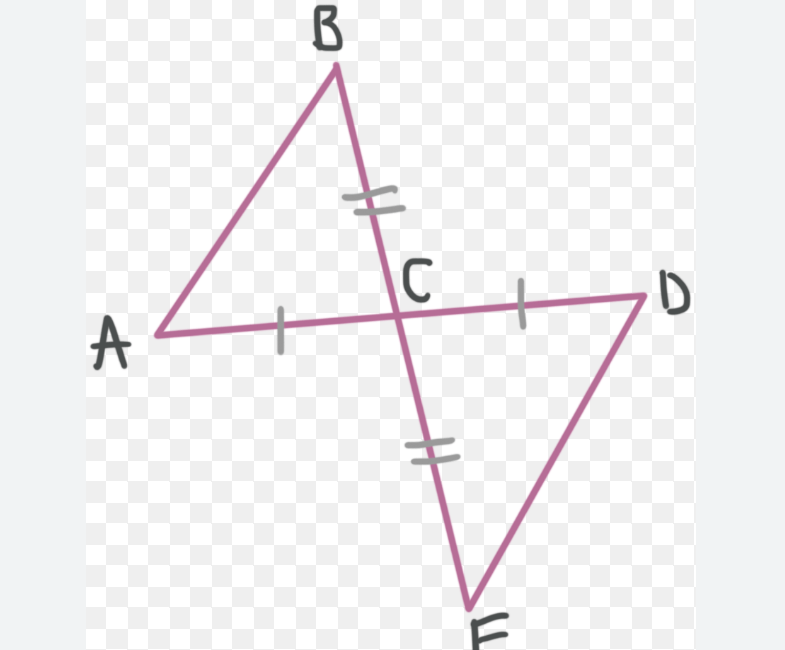
Which information is missing to prove SAS?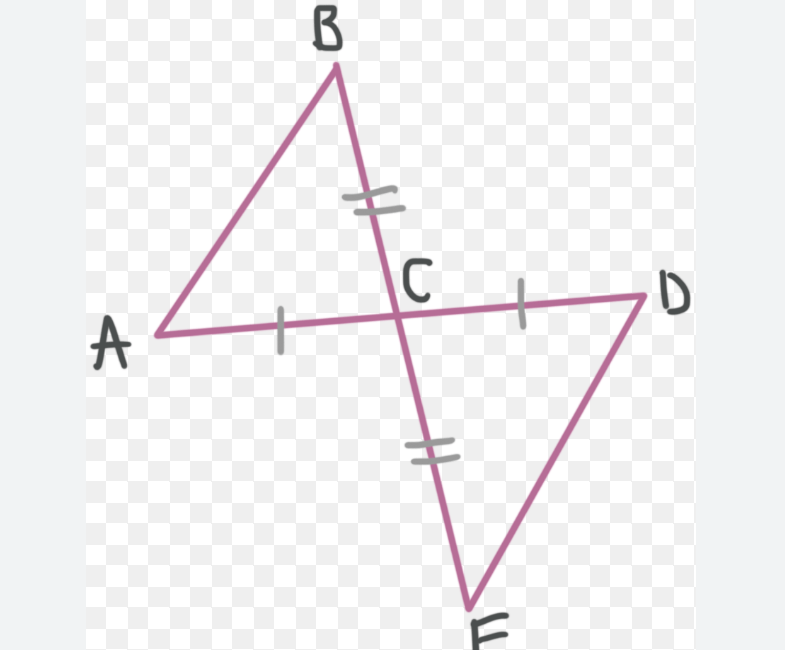
<BCA ≅ <ECD
or
<ACB ≅ <DCE