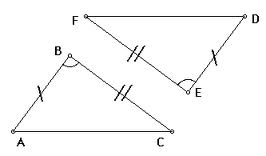
 Are these 2 triangles congruent?
Are these 2 triangles congruent?
Yes, they are congruent by SAS
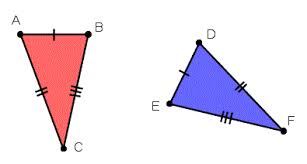
Assume:
C is the midpoint of BD and AE
What are the three relationships that prove the triangles congruent?
BC congruent to CD (since C is the midpoint)
AC congruent to CE (since C is the midpoint)
<BCA congruent to <DCE (vertical angles)
SAS
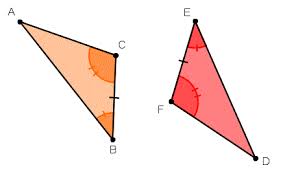
 Are these two triangle congruent?
Are these two triangle congruent?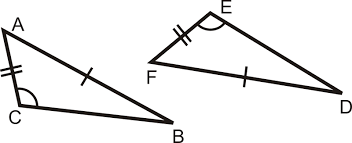 Is this proved by SSS?
Is this proved by SSS?What does "CPCTC? stand for?
Corresponding Parts of Congruent Triangles are Congruent
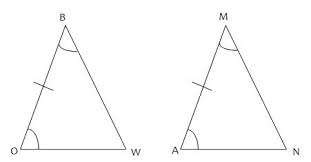
 Which postulate proves that these two triangles congruent?
Which postulate proves that these two triangles congruent?Are these triangles congruent?
Yes, the triangles are congruent by SSS
Assume:
DA congruent to DC
AB congruent to CB
What three congruent statements prove the triangles congruent, and what theorem proves the triangles congruent?
DA congruent to DC (Given)
AB congruent to CB (Given)
DB congruent to DB (Reflexive
SSS
DAB congruent to DCB
Are these triangles congruent by SSS?
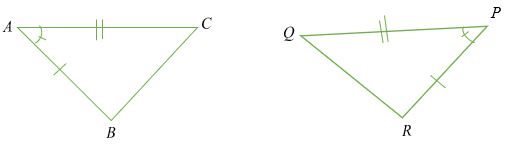
No, they are congruent by SAS
Assume:
A is the midpoint of ED and BC.
What three statements prove the triangle congruent, and what theorem proves the triangles congruent?
EA congruent to DA (since A is the midpoint)
BA congruent to AC (since A is the midpoint)
<EAC congruent to <BAD (Vertical Angles)
SAS
Are these triangles congruent by ASA?

No
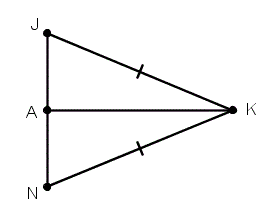
What three postulates prove the triangles congruent?
SAS
ASA
SSS
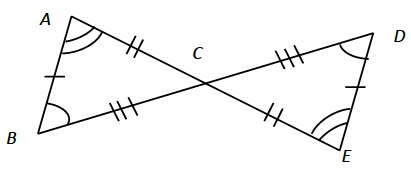
Are these triangles congruent? If so, write a congruency statement.
What is
triangleABCcongtriangleEDC