What is the complementary angle to 42.6 degrees?
47.4 degrees
Remember Complementary Angles add up to 90 degreesWhat is the measure of angle B?
Congruent
What is the measure of angle B?

< B = 28 degrees
Are the figures similar? Why?
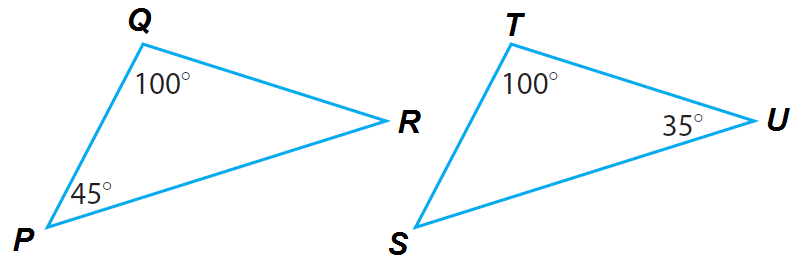
Yes, all three of their angles are congruent
What is the supplementary angle to 87.1 degrees?
92.9 degrees
Remember supplementary angles add up to 180 degrees.
What is the measure of angles 1 and 2?
< 1 = 18 degrees
< 2 = 162 degrees
What angle pair are angles 3 and 5?
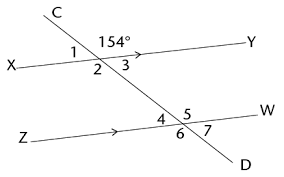
Same Side Interior
Solve for angle x

x = 70 degrees
The sum of the two interior angles always equals the exterior angle
Are the following similar? Why?
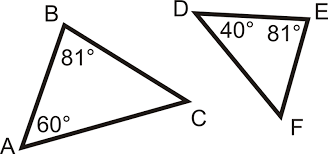
No, not every angle is congruent
True or False:
Vertical Angles are always congruent.
True
Vertical angles always equal the same measurement, congruent just means equal
What is the measure of angle 5 and angle 1?

< 5 = 154 degrees
< 1 = 26 degrees
What are the angle pair names that a transversal creates.
There's 6 of them!
Vertical, Corresponding, Alternate Interior, Alternate Exterior, Same Side Interior, and Same Side Exterior
Solve for x.
x = 5
13x+ 16x + 7x = 180 Combine Like Terms, solve for x
True or False:
Two shapes are similar when they have the exact same size, but not the same shape.
True, the angles all need to be the same. When we dilate shapes they stay similar to the Pre-image
If <x, <y, and <z are all supplementary to each other, find the measure of <z
<x = 53.1
<y = 32.7
<z = ?
< z = 93.2 degrees
Remember supplementary angles add up to 180 degrees. So <x + <y + <z = 180
Solve for x:
x = 19
<4 equals 134.8 degrees
Remember Alternate Exterior angles are congruent, making <3 and <4 equal to one another
Solve for angle Z
49
Solve for h. Separate the two triangles to help you
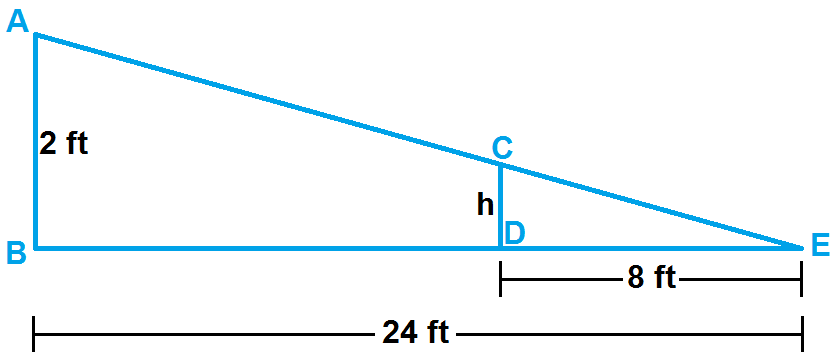
h = 2/3
If <h and <g are complementary to each other, what would <h equal if <g is 69.7 degrees?
<h equals 20.3 degrees
Remember complementary angles add up to 90 degrees
What is the measure of the two angles?
122 degrees
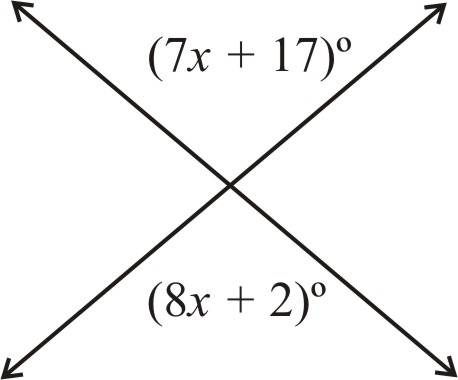
Set them both equal to each other, then solve for x
Name three pairs of corresponding angles:

<1 and <4
<2 and <6
<3 and <7
154 degrees and <5
If Triangle ABC had the following angles, find the measure of angle C
< A = 13.6 degrees
< B = 109.2 degrees
< C =?
< C = 57.2 degrees
Solve for the missing side. Separate the Triangles first
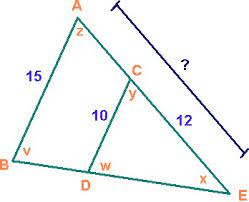
? = 18
