Basics
Types of congruence
Proofs
100
Which triangle is NOT congruent to the other three?
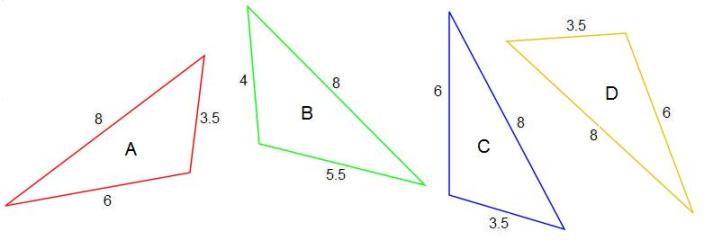
Triangle B.
100
State the postulate that proves the triangles together?
ASA (Angle Side Angle)
100
Gina has designed two triangular flower beds, as shown below. Which statement is true for the two flower beds?
a. They have the same perimeter.
b. The length of side PQ is equal to 10 feet.
c. The length of side BC is equal to 10 feet.
d. They have different areas.
Option A.
They are congruent and their sides will be of same lengths.
200
1. What is the difference between Similarity of Triangles and Congruence of Triangles?
2. If two triangles are congruent, are they also similar?
1. Similar triangles have the same shape, but may not have the same size. Congruent triangles have the same shape as well as the same size.
2. Yes. All congruent triangles are also similar.
200
State the postulate that proves the triangles together?
AAS (Angle Angle Side)
or
ASA (Angle Side Angle)
200
Is AAA a sufficient condition to show congruence between two triangles? Why or Why not?
No. Two triangles can have the same angles but different sizes.
300
The two triangles are congruent. What is the perimeter of triangle XYZ?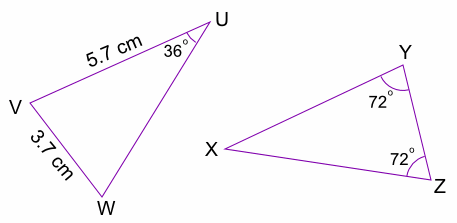
VU = XZ = 5.7 cm
VW = ZY = 3.7 cm
XY = XZ = 5.7 cm (isosceles triangle)
Perimeter = 15.1 cm
300
Name all the types of congruences.
1. SSS
2. SAS
3. ASA
4. AAS
5. RHS
300
In an Isosceles triangle ABC with AB = AC, AD is a perpendicular from vertex A to side BC.
Prove that D is the mid point of the side BC.
Triangles ABD and ACD are congruent, but RHS condition.
R: Angle ADB = Angle ADC = 90 (since AD is perpendicular)
H: AB = AC (Given)
S: AD = AD (common side)
Therefore BD = CD
=> D is the mid point of BC.