All Student Take Calculus
Exact Values
SOHCAHTOA
Law of Sines & Cosines
Miscellaneous
100
For which quadrants are cos positive?
1 and 4
100
Find cos(45o)
1/root(2)
100
Define Sin, Cos, Tan in terms of opp, adj, hyp.
Sin=opp/hyp
Cos=adj/hyp
Tan=opp/adj
100
State one of the Laws of Cosine and the Law of Sines.
a2=b2 + c2-2bccos(A) or
b2=a2 + c2-2accos(B) or
c2=a2 + b2-2abcos(C)
and
Sin(A)/a=Sin(B)/b=Sin(C)/c
100
Find two coterminal angles, one positive, one negative of 115o.
115o-360o = -245o
115o+360o = 475o
200
For which quadrants are sin positive?
1 and 2
200
Find sin(30o)
1/2
200
Define Sec, Csc, Cot in terms of opp, adj, hyp.
Sec=hyp/adj
Csc=hyp/opp
Cot=adj/opp
200
Solve for a if b=12, c=24, and angle A=40o.
a2 = 122+242-2(12)(24)cos(40o)
a = 16.7
200
If sin= 5/13, find cos
and tan
.
cos=12/13
tan=5/12
300
For which quadrants are cot positive?
1 and 3
300
Find cos(30o)
root(3)/2
300
Find the length of the opposite side.
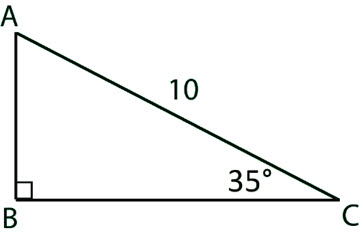
10sin(35o) = 5.74
300
Solve for angle B if a = 7, b = 10, and c = 4.
102 = 42+72-2(4)(7)cos(B)
angle B = 128.7o
300
Find all six trig functions of an angle A whose terminal side passes through the point (-2,5).
tanA = 5/-2 cotA = -2/5
cosA = -2/root(29) secA = root(29)/-2
sinA = 5/root(29) cscA = root(29)/5
400
For which quadrants are sec negative?
2 and 3
400
Find tan(135o)
-1
400
Find the length of the hypotenuse.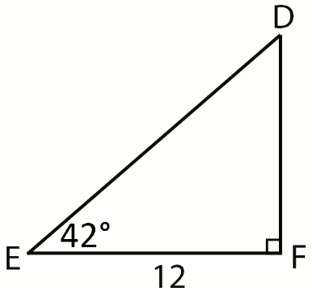 
12/cos(42o) = 16.15
400
Solve for a if b=12, c=8, and angle B=40o.
Angle C = sin-1(8sin(40o)/12) = 25.4o
Angle A = 180o-40o-25.4o = 114.6o
a = 12sin(114.6o)/sin(40o) = 17
400
For what angle is the cotangent 2/3?
cot = 2/3, so tan = 3/2
tan-1(3/2) = 56.3o
500
For which quadrants are csc negative?
3 and 4
500
Find sin(300o)
-root(3)/2
500
Solve the entire triangle:
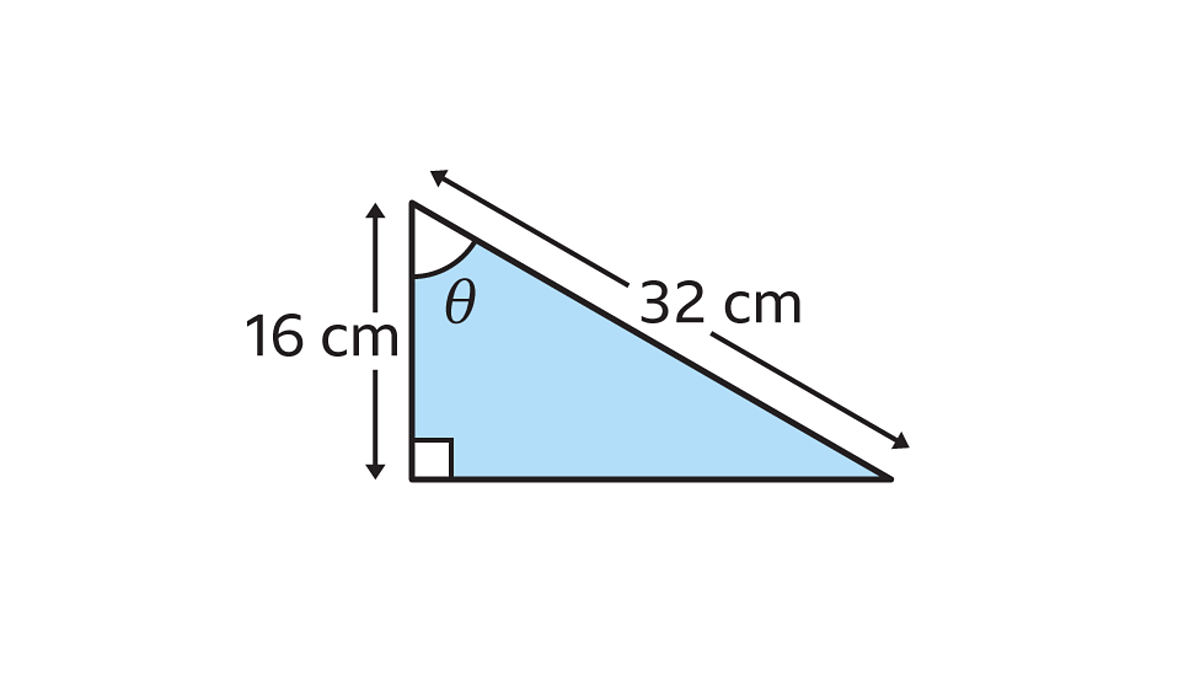
This is a 30o, 60o, 90o triangle, and the multiplier is 16. Thus, the missing side is 16root(3).
500
Solve the triangle completely: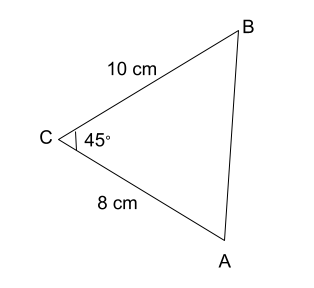 
c2 = 82+102-2(8)(10)cos(45o) = 7.1
Angle B = sin-1(8sin(45o)/7.1) = 52.8o
Angle A = 180o-45o-52.8o = 82.2o
500
Find the area of a triangle with side lengths 12 cm and 17cm, and an angle of 50o between them.
Use K=1/2(a)(b)sin(C)
1/2(12)(17)sin(50o) = 78.1 cm2