Special Right Triangles
Name that Ratio
Understand the Concept
Solve for x
Angle of Depression & Elevation
100
What are the two special right triangles?
45-45-90
30-60-90
100
To use sine, cosine, and tangent, your calculator must be in ______________ mode.
What is DEGREE mode?
100
______________________ ______________ have equivalent cosine and sine ratios.
What is COMPLEMENTARY angles?
100
What are ratios used to solve for? What are inverse ratios used to solve for?
Trig ratios are used to solve for missing SIDE LENGTHS on a right triangle while inverse trig ratios are used to solve for missing ANGLE MEASURES on a right triangle.
100
Alpha is an angle of _________________.
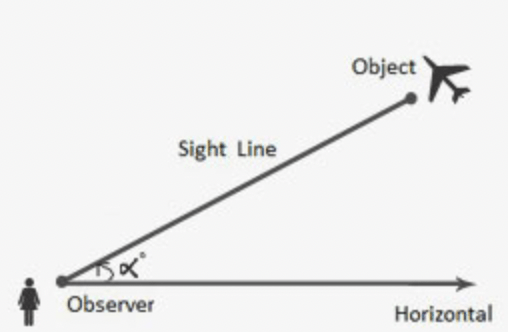
What is angle of ELEVATION?
200
What is x and y?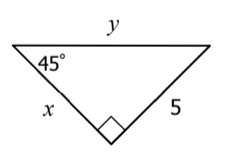
x = 5 and y = 5\sqrt{2}
Remember, the rules!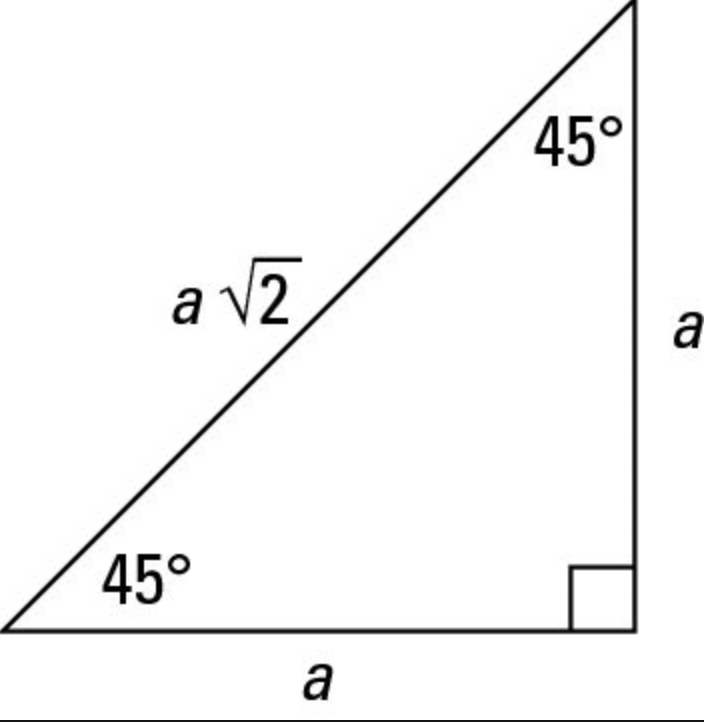
200
\frac{opposite}{hypotenuse}
What is sine?
200
Given that cos(26) = 0.899, what is sin(64)?
Complementary angles have equivalent sine and cosine angles, so sin(64) = cos(26) = 0.899.
200
Which ratio would you use in this equation to solve for x?
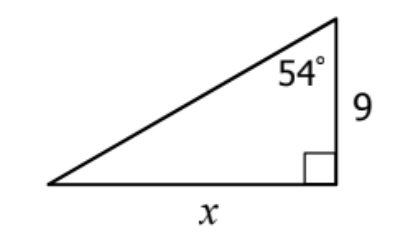
What is tangent?
tan(54) = \frac{x}{9}
200
What is the measure for x?
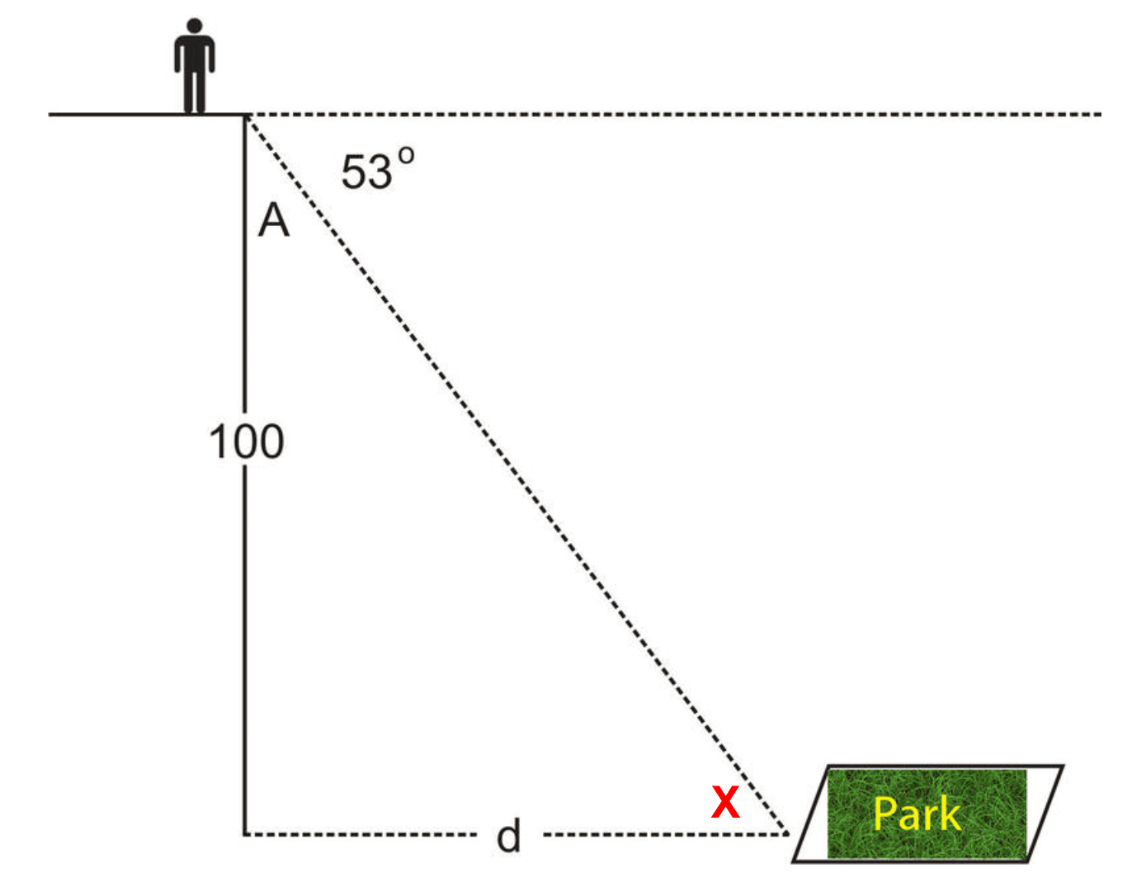
Since the angle of elevation is the same as the angle of depression, x = 53.
300
What is x & y?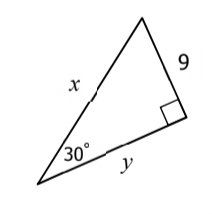
x = 18
y = 9\sqrt{3}
Remember the rules!
300
What is tan(X)?
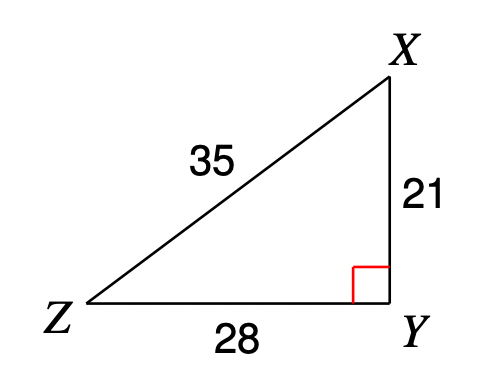
tan(X) = \frac{opposite}{adjacent} = \frac{28}{21} = \frac{7}{3}
300
Given two triangles, fill in the inequality that fits the statement
b/a _______ y/x
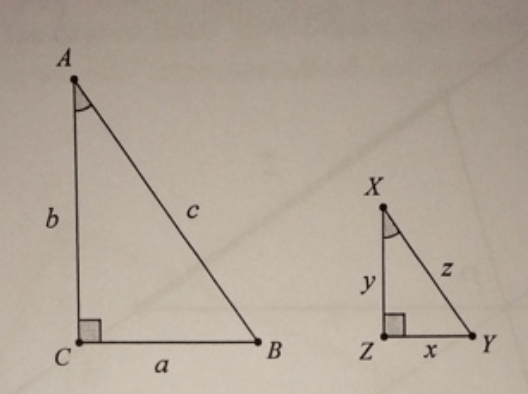
The two ratios are equal!
300
Solve for x.
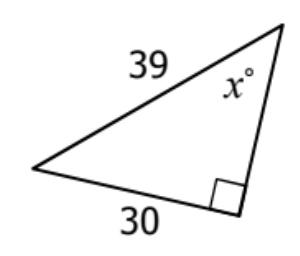
x = sin^{-1}(\frac{30}{39}) = 50.28486277
300
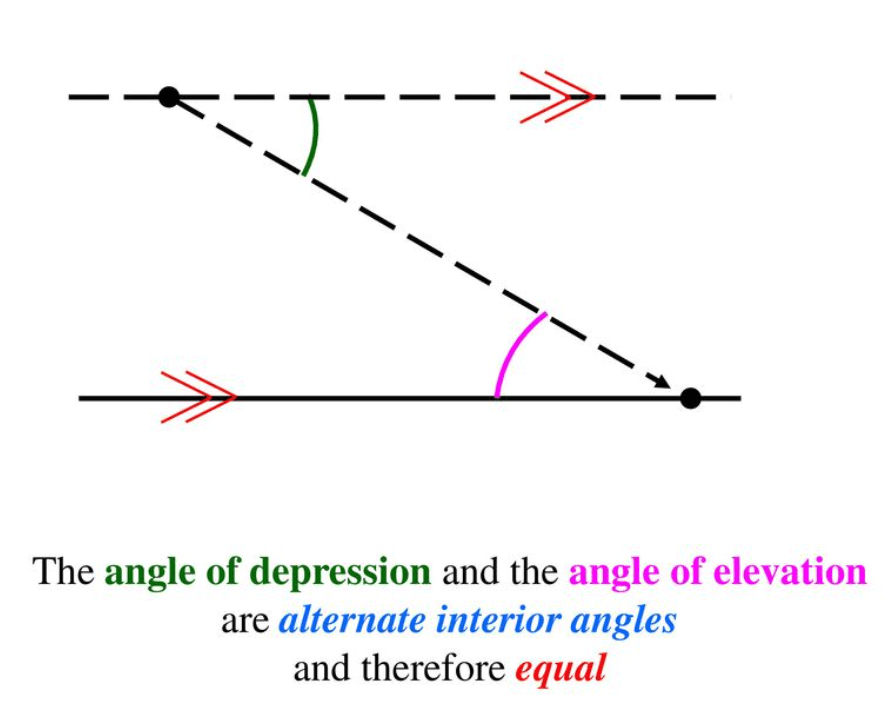
What theorem allows the angle of elevation to equal the angle of depression on a problem?
Alternate Interior Angles Theorem
400
What is x & y?
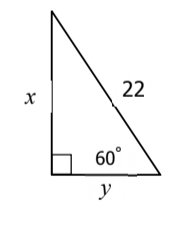
x = 11\sqrt{3}
y = 11
400
Find each trigonometric ratio. Give your answer as a fraction in simplest form.
To find the missing side, use Pythagoras!
16^2+30^2=c^2
1156=c^2
34=c
Now, find the ratios!
sin(Q) = \frac{30}{34} = \frac{15}{17}
cos(Q) = \frac{16}{34} = \frac{8}{17}
tan(Q) = \frac{30}{16} = \frac{15}{8}
400
The theorem that allows trig ratios to exist
AA~
As long as it is a right triangle with one more pair of congruent angles, all ratios within the triangle are congruent! Which is why we can use the trig ratios
400
Solve for x.
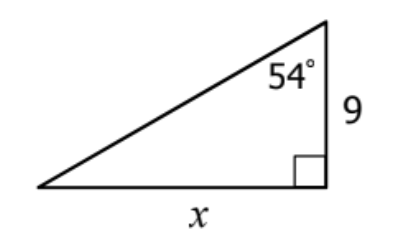
tan(54)=\frac{x}{9}
x = 9tan(54)
x = 12.38743728 = 12.4
400
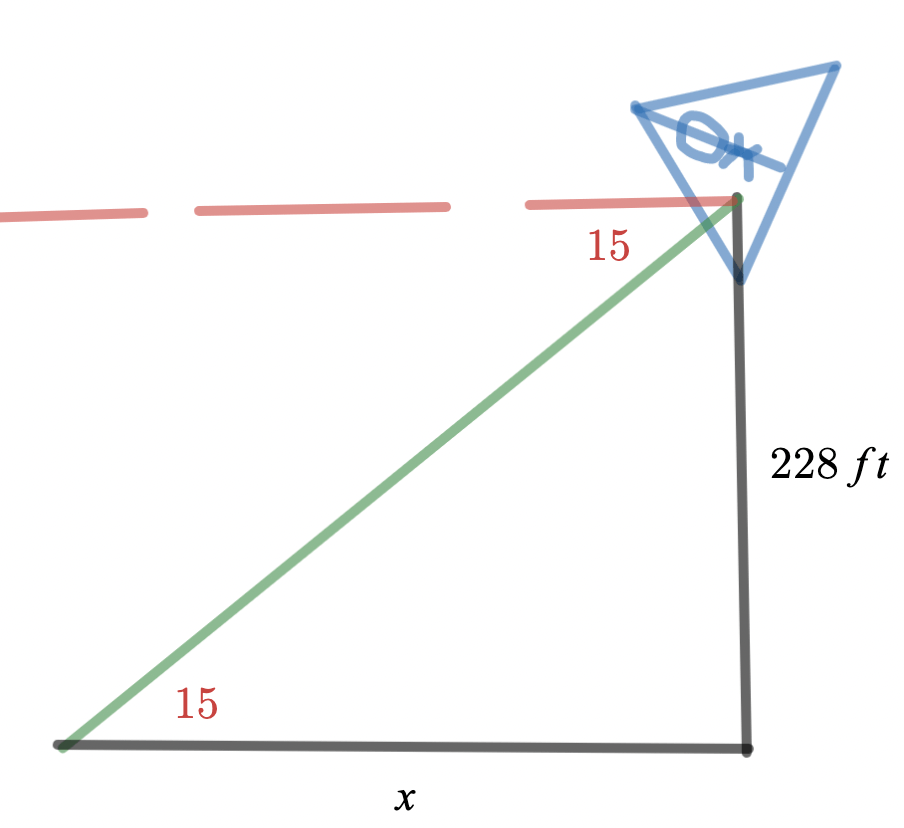
While parasailing, Ryan spots a dolphin on the water below. If Ryan is 228 feet above the water and the angle of depression to the dolphin is 15°, what is the horizontal distance between Ryan and the dolphin? Round to the nearest tenth.
tan(15) = \frac{228}{x}
xtan(15) = 228
x = \frac{228}{tan(15)} = 850.907584 = 850.9 ft
500
What is x & y?
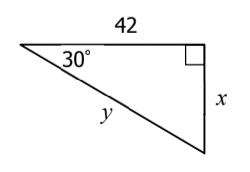
x = 14\sqrt{3}
y = 28\sqrt{3}
42=a\sqrt{3}
a = \frac{42}{\sqrt{3}}
a = \frac{42}{\sqrt{3}} * \frac{\sqrt{3}}{\sqrt{3}} = \frac{42sqrt3}{3}=14\sqrt{3}
500
Fill in the blank.
_______________(Z) =
\frac{4}{5}
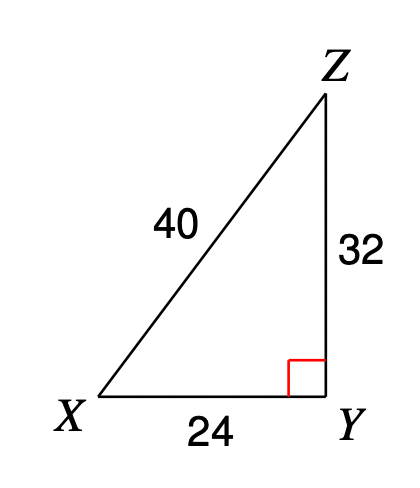
What is cosine?
500
Let
sin(32) = 0.52991926423.
What does the ratio mean on the following triangle? Where does that specific number come from?
Sine, cosine and tangent are ratios, and since triangles are similar, all triangles with a 32 degree angle will simplify to the EXACT SAME decimal.
Therefore, 0.5299292623 comes when you divide the opposite side by the hypotenuse side, specifically in reference to a 32 degree angle.
500
What is x?
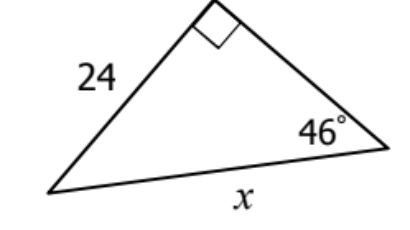
sin(46) = \frac{24}{x}
xsin(46) = 24
x = \frac{24}{cos(46)}
x = 33.36392618 = 33.4
500
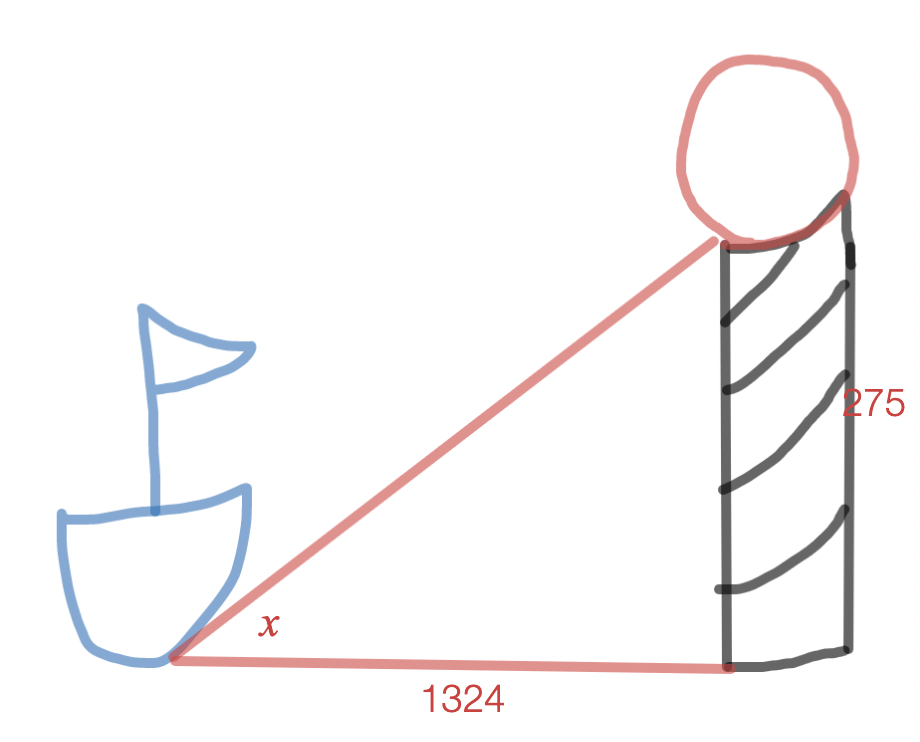
A boat is 1,324 feet from shore. If a 275 foot lighthouse is right on the shore, find the angle of elevation from the boat to the lighthouse.
x = tan^{-1}(\frac{275}{1324}) = 11.73372239 = 11.7
