Pythagorean Theorem 1
Pythagorean Theorem 2
Either
Trigonometry 1
Trigonometry 2
What does it mean?
100
When using the Pythagorean Theorem, the Hypotenuse is labeled with what letter?
c
100
When using the Pythagorean Theorem, the shorter sides are labelled with what letters?
a & b
100
When using Trigonometry, the side length across from the angle is labeled with what letter?
O
100
When using Trigonometry, the Hypotenuse is labeled with what letter?
h
100
When using Trigonometry, the side length across from the 90 degree angle is labeled with what letter?
H
100
What's special about the triangle with sides in ratio
1
2
sqrt3
It has the angles 30, 60, 90
200
When using the Pythagorean Theorem, what is the formula to calculate side c?
c=sqrt(a^2+b^2)
200
When using the Pythagorean Theorem, what is the formula to calculate side a?
a=sqrt(c^2-b^2
200
When using Pythagorean Theorem, what is the formula to calculate side b?
b=sqrt(c^2-a^2
200
sin (theta)=
o / h
200
cos(theta)=
a/h
200
What's special about the triangle with sides in the ratio 1
1
sqrt2
It has angles 45, 45, 90
300
Calculate the length of the hypotenuse:
26
300
Calculate the length of the Hypotenuse (to 2 dp):
7.62
300
Evaluate: tan(48) (to 2 decimal places)
1.11
300
Evaluate: sin(25) (to 2 decimal places)
0.42
300
Evaluate: cos(59) (to 2 decimal places)
0.52
300
What is the horizontal distance?
12.8
400
Calculate x (to 2 dp):
23.24
400
Calculate x (to 2 dp):
19.24
400
When using Trigonometry, what formula is used to calculate the opposite side when given the Hypotenuse?
o=h*sin(theta)
400
When using Trigonometry, what formula is used to calculate the adjacent side when given the Hypotenuse?
a=h*cos(theta)
400
When using Trigonometry, what formula is used to calculate the Hypotenuse when given the opposite side?
h=o /(sin(theta)
400
Penny can see the clock on the top of her town’s courthouse from her front yard. The clock is at a horizontal distance of 140 metres from her house. If the angle of elevation from where she stands in her yard to the clock is 15°, what is the elevation of the clock if her eye level is 1.6 metres above the ground? Round your answer to the nearest tenth.
39.1
500
What is the length of bd?
12
500
Daniel rides his bicycle 21 km west and then 18 km north. How far is he from his starting point? (to 2 dp)
27.66 km
500
Using Trigonometry, calculate the Hypotenuse when the Adjacent side = 31 and the angle = 48?
H = 46.33
500
Using Trigonometry, calculate the Hypotenuse when the Opposite side = 9 and the angle = 24?
H = 22.13
500
Using Trigonometry, calculate the opposite side when the Hypotenuse = 18 and the angle = 47?
O = 13.16
500
A lighthouse sits at the edge of a cliff, as shown. A ship at sea level is 610 metres from the base of the cliff. The angle of elevation from sea level to the base of the lighthouse is 55.1°. The angle of elevation from sea level to the top of the lighthouse is 56.5°. What is the height of the top of the lighthouse to the cliff?
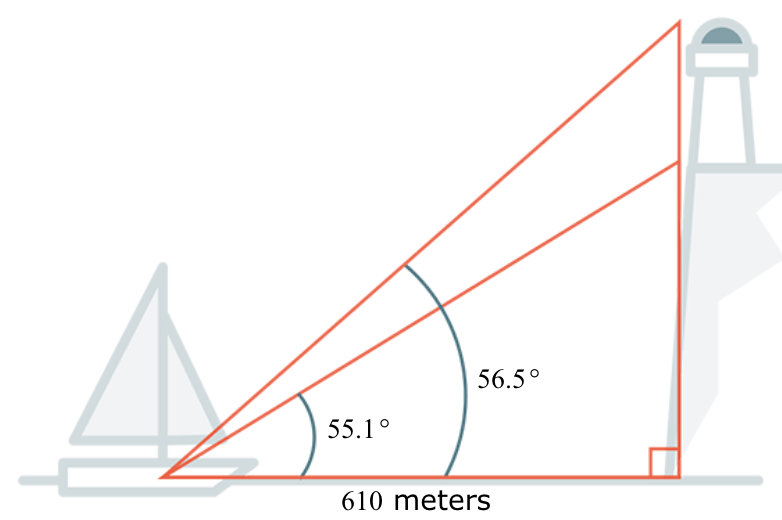
47.2