Graphs
Unit Circle
Inverse Trig
Degrees and Radians
Trig Identities
100
Which trig functions have vertical asymptotes at
x=pi/2+pi*n, n=ZZ
tangent and secant
100
What quadrant is the following angle in?
-(3pi)/4
3rd quadrant
100
Why is the domain of a trig function restricted when finding the inverse?
A function must be one-to-one (pass the horizontal line test) for its inverse to be a function.
100
What is the degree measurement for an angle of
(7pi)/4
315^o
100
Why is the following equal to one?
sinx*cscx
a function multiplied by its reciprocal equals 1
200
Is the following periodic, sinusoidal, or both?
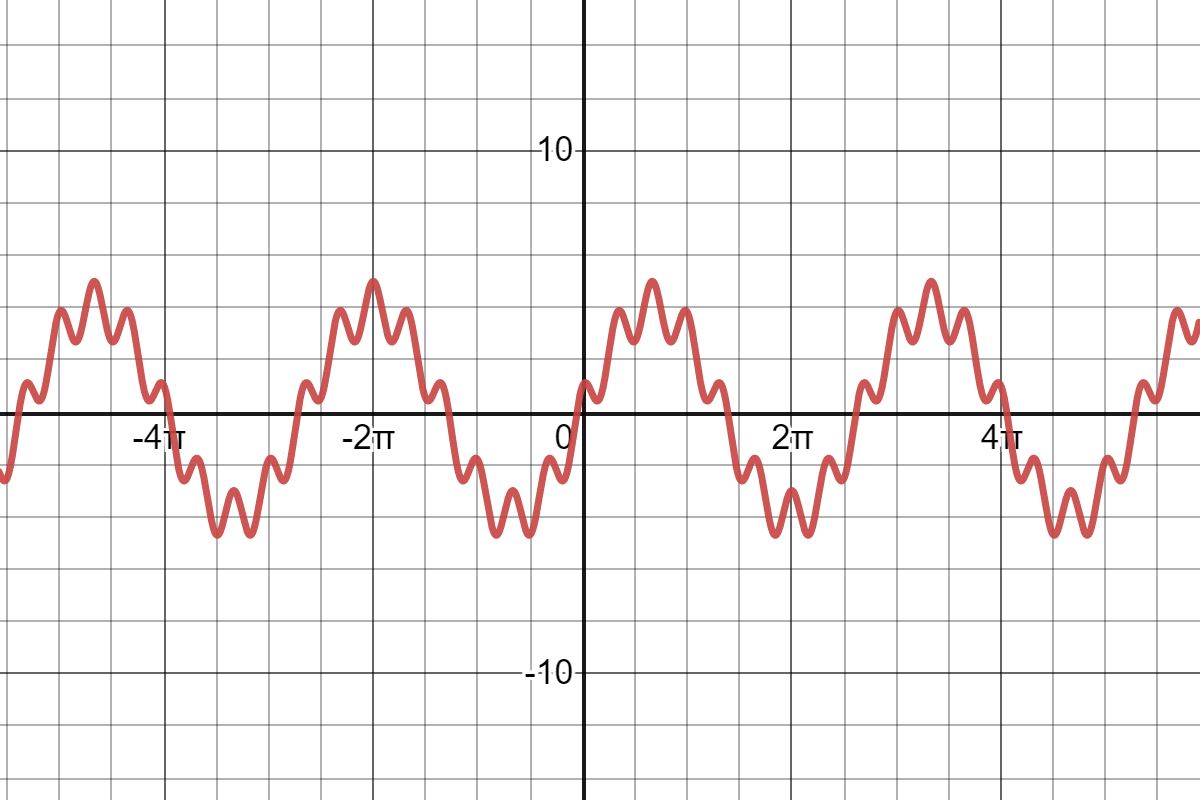
Periodic, not sinusoidal
200
Which trig functions are negative in the 2nd quadrant?
Cosine, Secant, Tangent, Cotangent
200
Which inverse trig function has the following graph?
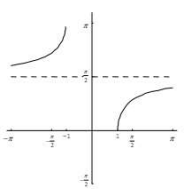
arcsec(x)
200
What is the radian measurement for the given angle?
225^o
(5pi)/4
200
Write the following in terms of its cofunction:
tan(28^o)
cot(62^o)
300
The _______ of cosine match up with the ______ of secant.
max's/min's......min's/max's
300
What is the smallest positive coterminal angle to
-(2pi)/3
(4pi)/3
300
Evaluate the following:
arctan(tan(pi))
0
300
What is the range of arcsec(x)?
0<=x<=pi
300
What is the pythagorean trig identity that involves tangent?
tan^2x+1=sec^2x
400
What two functions would bound the following function?
y=2x-2cosx
y=2x-2 and y=2x+2
400
Evaluate:
sec((4pi)/3)
-2
400
Evaluate the following:
arccos(sin((5pi)/3))
(5pi)/6
400
Cofunctions of angles that add up to ____ are equal.
90 degrees or pi/2
400
Simplify the following expression using a negative angle identity:
csc(-x)*tan(x)
-sec(x)
500
Create the equation of a function that IS sinusoidal.
answers vary
y=asin(bx)+-dcos(bx)
500
Given that...
sec(theta)<0
tan(theta)=-9/2
What is...
cos(theta)
cos(theta)=-(2sqrt85)/85
500
E
artctan(-sqrt3/3)
valuate:
-pi/6 or (11pi)/6
500
About how many degrees is one radian?
57.3 degrees
500
Simplify the following trigonometric expression:
(sin^2x)/(1-cosx)-cosx
1