Unit Circle
Inverse Trig Functions
Graphs
Word Problems
100
cot({5pi}/6)=
-sqrt{3}
100
cos^{-1}(1/2)
pi/3
100
The following graph has the equation A+Bsin(Cx) where A,B and C may be positive or negative. Find A,B and C.
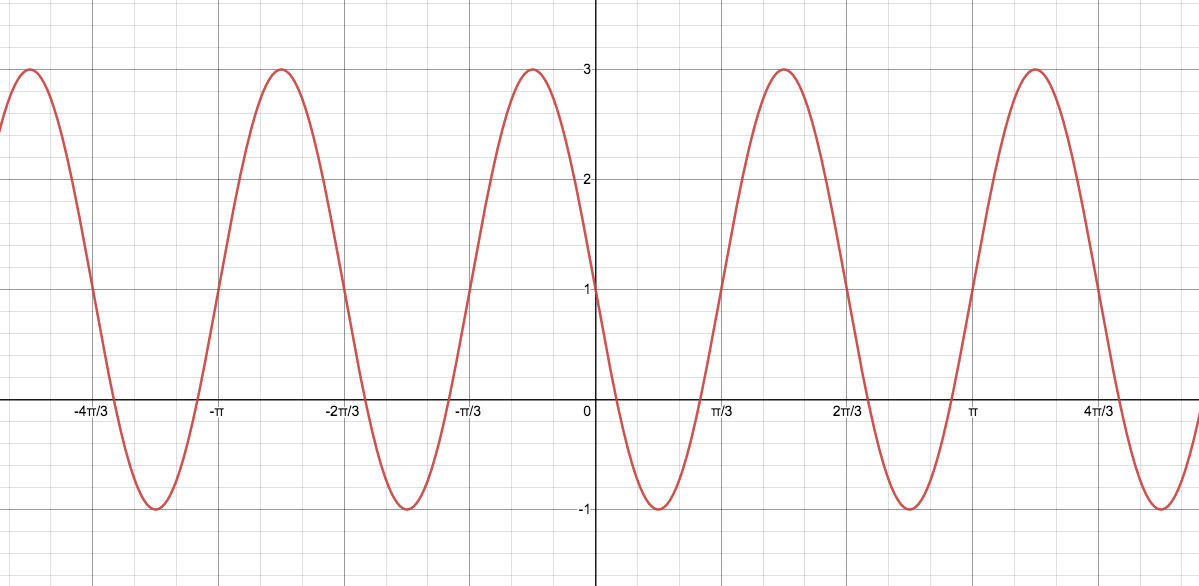
A=1,B=-2,C=3
100
The water level of the sea of serendipity varies sinusoidally with equation
pi+2cos(3pix-pi/2)
there t is the number of hours since midnight. What is the first time that the sea level is at a minimum?
t=1/2
200
If
tan(theta +pi/2)=a
find
tan(theta - pi/2)
in terms of a
a
200
sec^{-1}({-2sqrt{3}}/3)
{5pi}/6
200
The following graph has the equation A+Bcos(C(x+D)) where A,B,C and D may be positive or negative. Find A,B,C, and D.
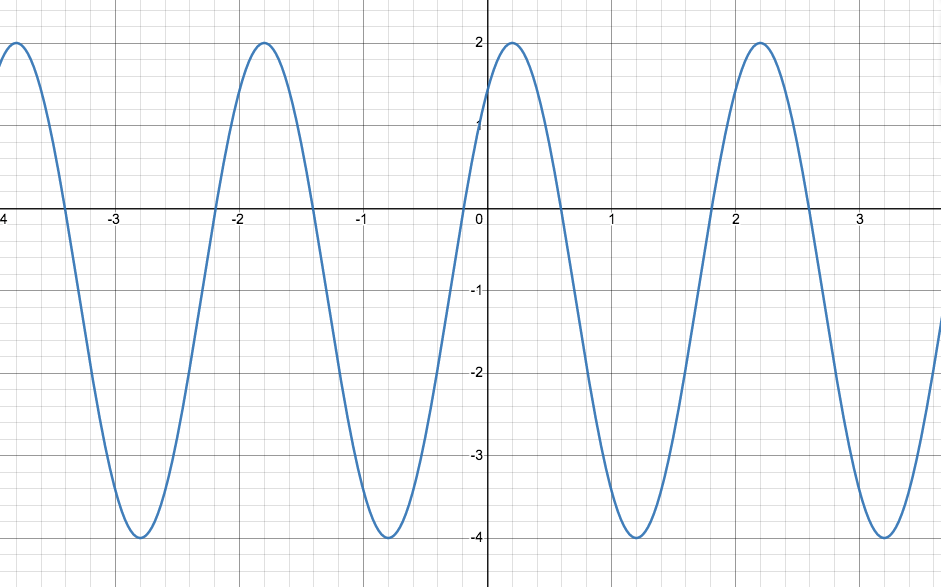
A=-1,B=3,C=pi,D=-pi/5
200
Proofy McYoYoPants is a very nice Proofnik who uses a yo-yo the way they are intended to be used (going up and down). Suppose that Proofy's yo-yo's height is a sinusoidal function and that it take 2 seconds to go from the bottom of the string to the top. Proofy releases the yo-yo at the top of the string and after half a second, it is exactly 3 feet off the ground. How many seconds does it take until the yo-yo is next exactly 3 feet off the ground?
3 seconds
300
Arrange the following in order from smallest to largest:
cos({5pi}/11),cos({6pi}/11),sin({pi}/3),sin({5pi}/4)
sin({5pi}/4),cos({6pi}/11),cos({5pi}/11),sin({pi}/3)
300
csc(tan^{-1}(3/7))=
sqrt{58}/3
300
Write a possible equation for the following graph:
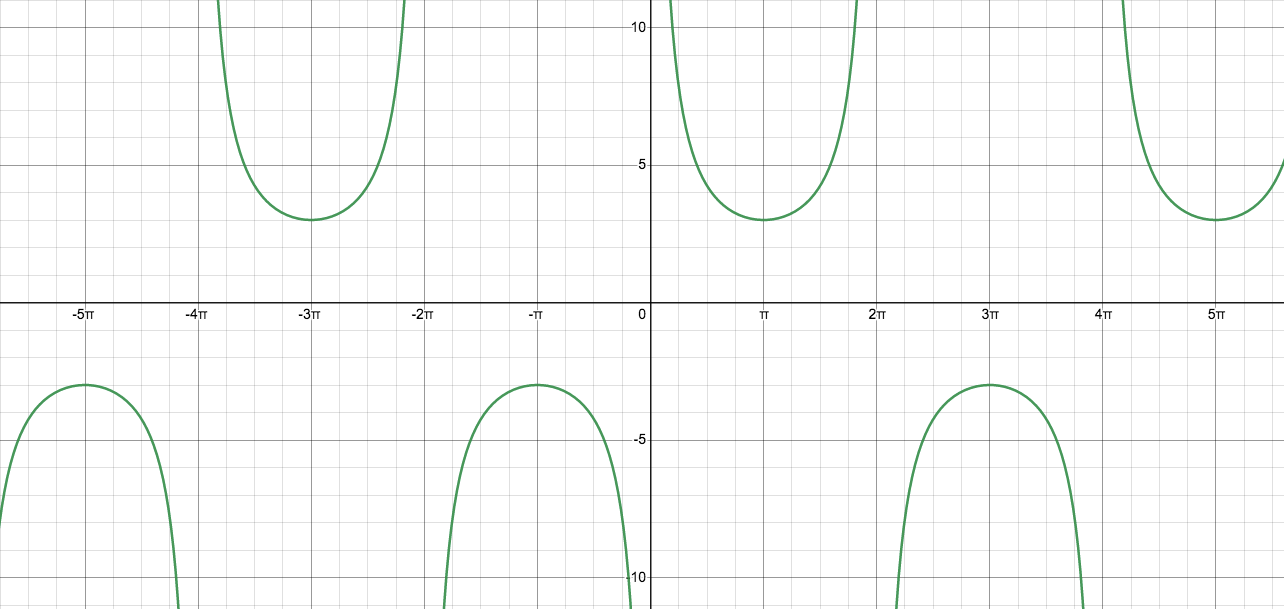
3csc(x/2)
300
The planet Zorp has 16 hour days, and the planet’s temperature varies sinusoidally with a minimum temperature of 70 degrees two hours before sunrise and a maximum temperature of 110 degrees, six hours after sunrise. You arrive on the planet four hours after sunrise. How much later does the temperature hit exactly 80 degrees? Give your answer in exact hours and minutes. No calculators.
7 hours and 20 minutes after you arrive.
400
If
sin({3pi}/8)=a
find
cos({5pi}/8)
in terms of a.
-sqrt{1-a^2}
400
cos(cot^{-1}(sin({7pi}/6)))=
{-sqrt{5}}/5
400
Find positive numbers A and B such that the equations
sin(-2(x-pi/6))
and
cos(Ax+B)
describe the same graph.
A=2, B=pi/6
400
I'd like to lift my bike wheel to my ceiling for storage so I've built a pulley to lift it for me. The pulley has a radius of 1 foot and is mounted on the ceiling and my bike has a radius of 2 feet and is resting on the ground. The rope is tied at the center of the wheel. When I start to pull the rope, the pulley's wheel turns at a rate of 2 rotations per second, and somehow the wind causes the bike wheel to rotate as well, at a rate of 4 rotations per second. A piece of glitter on the ground directly below the wheel at the start gets stuck to the wheel. Write an equation for the height of the glitter after t seconds of my pulling the rope.
4pit+2-2cos(8pit)