Right Triangle Trig
Law of Sines
Law of Cosines
Story Problems
100
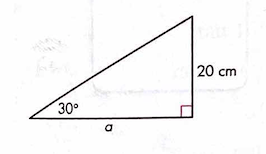
Solve for a using trigonometry.
a = 34.6 cm
100
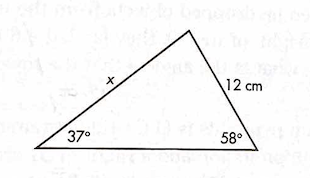Solve for x using the law of sines.
x = 16.9 cm
100
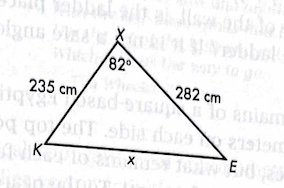Solve for x using the law of cosines.
x = 341 cm
100
A cargo company needs to load truck trailers into ship cargo containers. The trucks must drive up a ramp to a loading platform 30 feet off the ground, but they have difficulty driving up a ramp at an angle steeper than 20°. How long does the ramp need to be?
The ramp must be at least 87.7 feet long.
200
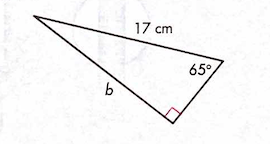Solve for b using trig.
b = 15.4 cm
200
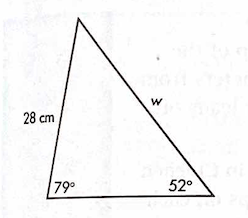Solve for w using the law of sines.
w = 34.9 cm
200
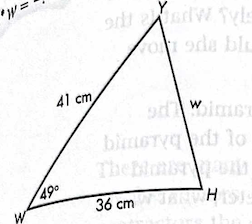
Solve for w using the law of cosines.
w = 32.3 cm
200
The angle of elevation from a ship to the top of a 42-meter lighthouse on the shore measures 33°. How far is the ship from the shore?
The ship is around 64.7 meters away.
300
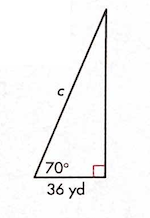Solve for c using trig.
c = 105.3 yd
300
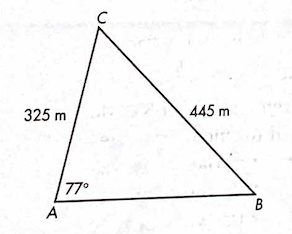Solve for B. Round to the nearest tenth.
B = 45.4 degrees
300
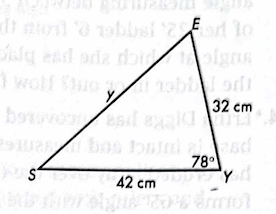Solve for y using the law of cosines.
y = 47.2 cm
300
Ben is flying a kite directly over his buddy Franklin, who is 125 meters away. His kite string makes a 39° angle with the level ground. How high is the kite?
About 101.2 meters high.
400
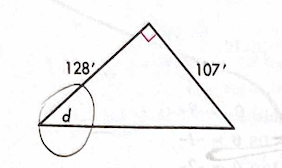Solve for d using trig.
d = 39.9 degrees
400
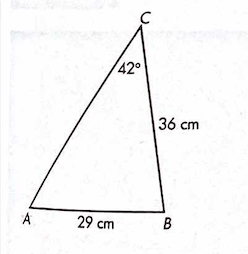Solve for A using the law of sines. Round to the nearest tenth
A = 56.2 degrees.
400
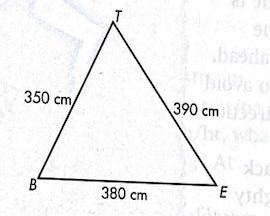Solve for B using the law of cosines.
B = 64.4 degrees
400
Bailey is flying a plane for Air International that just took off from the Sacramento International Airport. Bailey earns a big bonus if he hits the ideal takeoff angle for Air International flights, between 30° and 50° . Bailey’s plane is currently 500 feet off the ground and 400 feet from the spot where it took off. Did Bailey earn his bonus? If not, how close was he to the ideal takeoff angle?
He is at a takeoff angle of 51.3°, which is too high to earn a bonus.
500
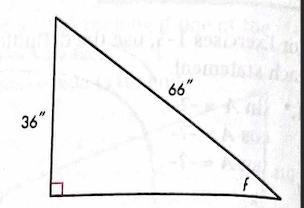Solve for f using trig.
f = 33 degrees.
500
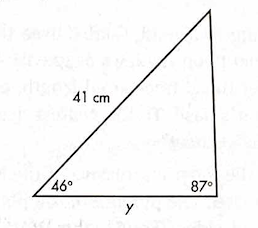Solve for y using the law of sines.
y = 30 cm
500
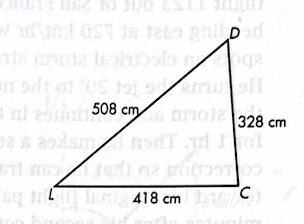Solve for C using the law of cosines.
C = 84.9 degrees
500
Mr. Jaime is looking to run a string of flags from the top of the soccer field lights to the ground below in celebration of the first soccer game of the season next year. If the string of flags are 100 feet long and are attached to the ground at a 36° angle, how tall are the field lights?
The field lights are 58.8 feet tall.