L1
L2
L3
L4
100
A tennis ball is dropped from a certain height. The graph below shows its height h in centimeters after t seconds. What is the ball's initial height?
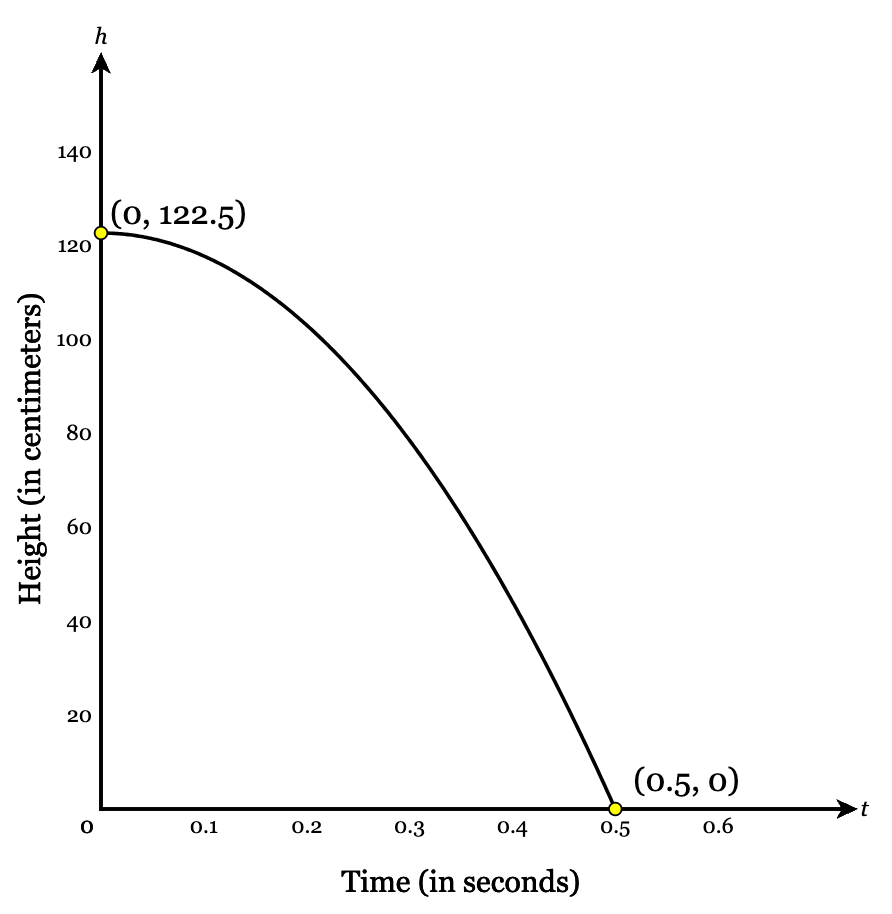
122.5 centimeters
100
Tallulah launches a toy rocket from a platform. The height of the rocket in feet is given by
h(t)=-16t^2+24t+16
where t represents the time in seconds after launch. What is the rocket’s initial height?
The rocket's initial height is 16 feet
100
The width of a rectangle is 3 units less than the length. The area of the rectangle is 54 square units. What is the length, in units, of the rectangle?
length=9
100
Solve the following inequality algebraically.
x^2+9x-10≤0
−10≤x≤1
200
A rocket is launched in the air. The graph below shows the height of the rocket h in meters after t seconds. What is the rocket’s greatest height?
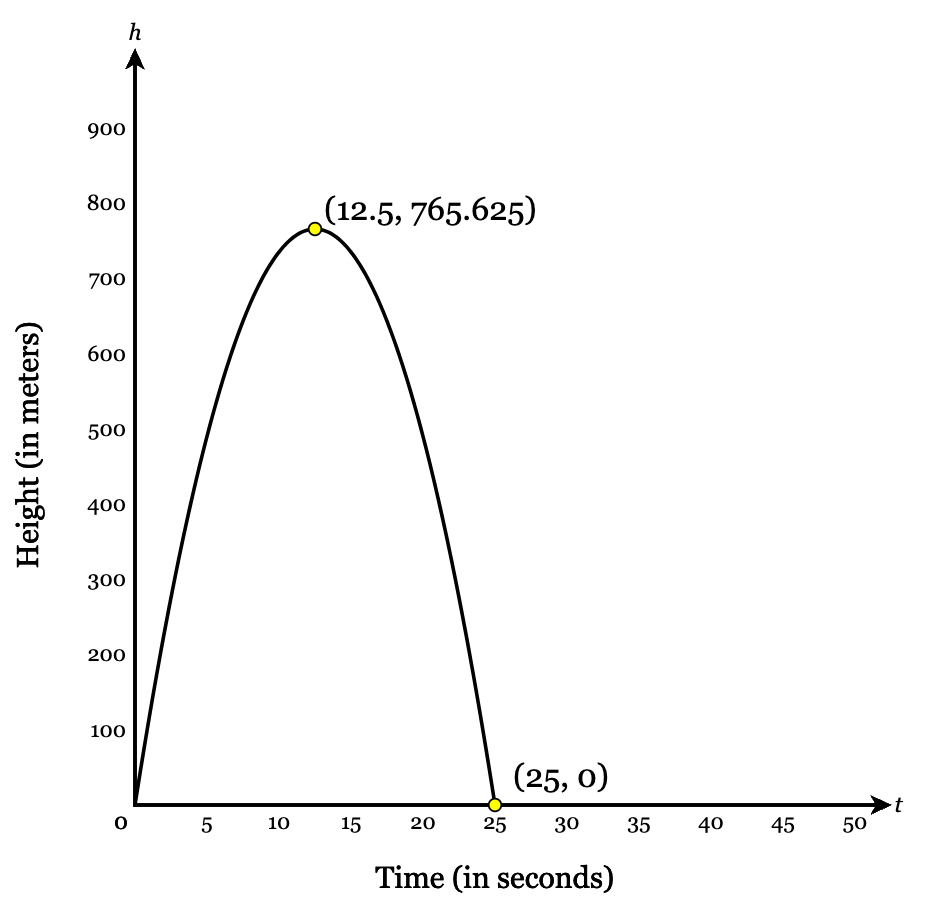
765.625 meters
200
Austin launches a toy rocket from a platform. The height of the rocket in feet is given by
h(t)=-16t^2+128t+68
where t represents the time in seconds after launch. What is the rocket’s greatest height?
The rocket's greatest height is 324 feet.
200
The difference of the square of a number and 18 is equal to 3 times that number. Find the positive solution.
Positive Solution: 6
200
Solve the following inequality algebraically.
x^2+7x-30≥0
x≤−10 or x≥3
300
Gavin kicks a football. The graph below shows the height of the football h in feet after t seconds. How many seconds have gone by when the football is at its highest point?
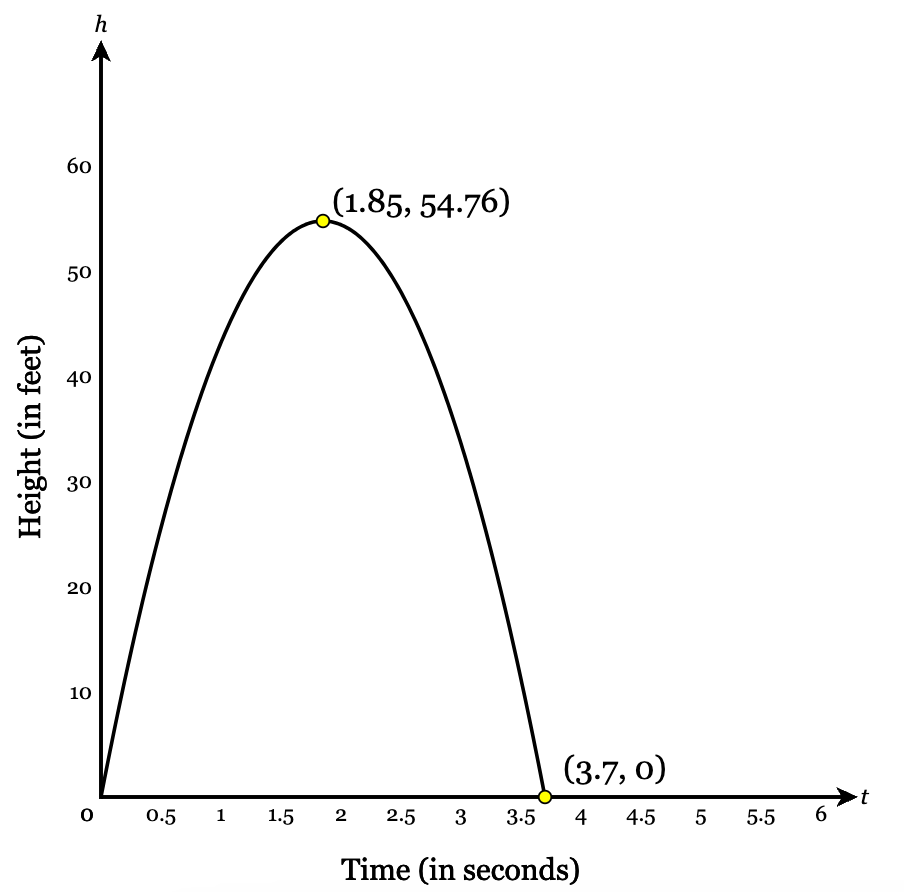
1.85 seconds have gone by when the football is at its highest point
300
A rocket is launched in the air. Its height in feet is given by
h(t)=-16t^2+112t
where t represents the time in seconds after launch. How many seconds have gone by when the rocket is at its highest point?
3.5 seconds have gone by when the rocket is at its highest point.
300
The width of a rectangle is 7 units less than the length. The area of the rectangle is 8 square units. What is the length, in units, of the rectangle?
length=8
300
Solve the following inequality algebraically.
x^2+2x-80>0
x<−10 or x>8
400
Fwam launches a toy rocket from a platform. The graph below shows the height of the rocket h in feet after t seconds. Find the interval for which the rocket’s height is increasing.
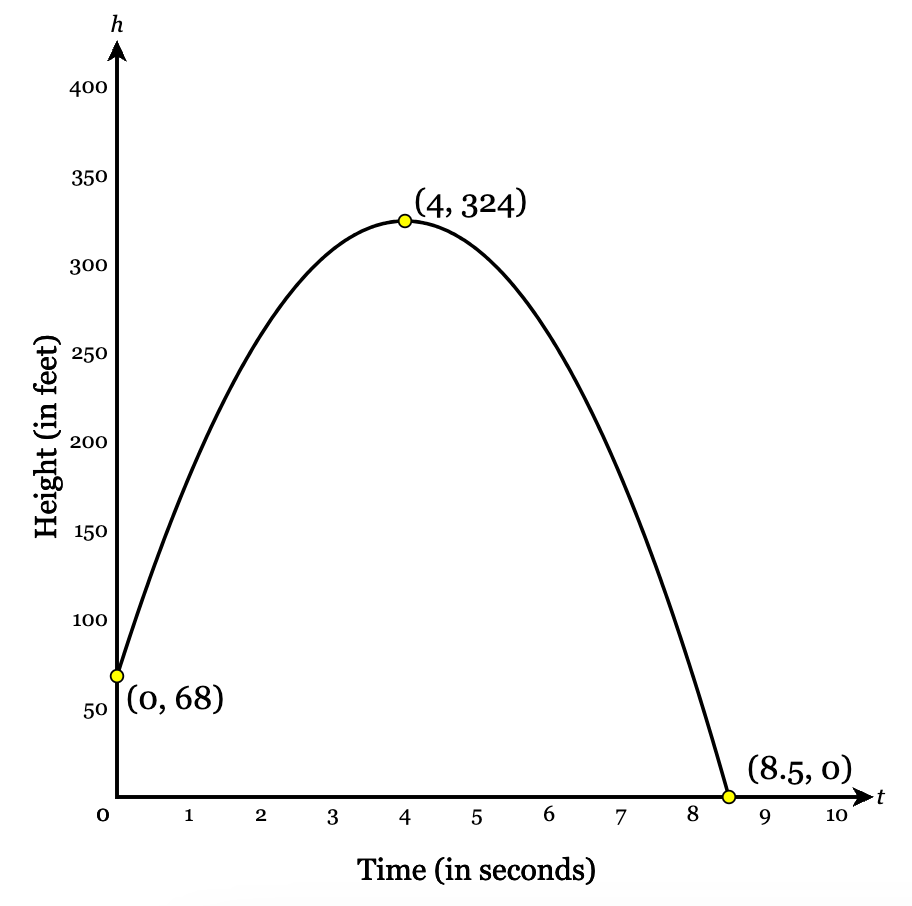
0<t<4
400
A rocket is launched in the air. Its height in feet is given by
h(t)=-16t^2+24t
where t represents the time in seconds after launch. How long is the rocket in the air?
The rocket is in the air 1.5 seconds.
400
The difference of the square of a number and 36 is equal to 5 times that number. Find the positive solution.
Positive Solution: 9
400
Solve the following inequality algebraically.
2x ^2 −27x+55≥−3x−9
x≤4 or x≥8
500
Jamal throws a ball up in the air. The graph below shows the height of the ball h in feet after t seconds. After how many seconds does the ball hit the ground?
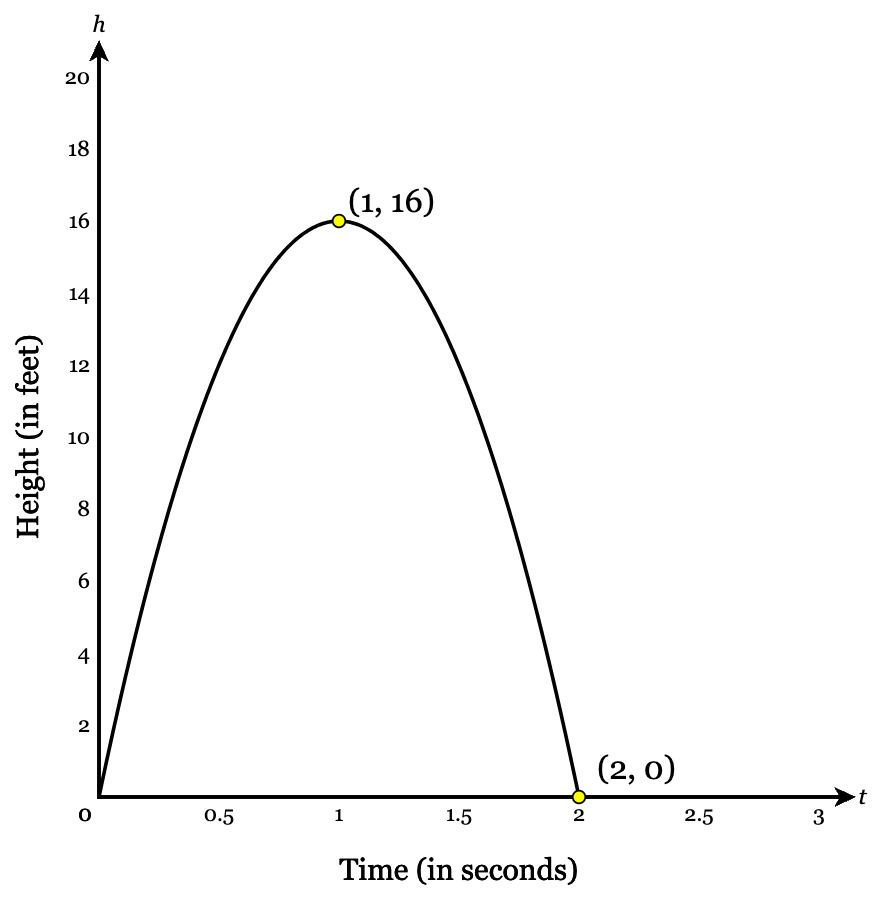
The ball hits the ground after 2 seconds
500
A rocket is launched in the air. Its height in feet is given by
h(t)=-16t^2+56t
where t represents the time in seconds after launch. How many seconds have gone by when the rocket is at its highest point?
1.75 seconds have gone by when the rocket is at its highest point.
500
The product of two consecutive positive integers is 110. Find the value of the greater integer.
The greater integer = 11
500
Solve the following inequality algebraically.
4x ^2 +9≥−8x+6
x≤−3/2 or x≥−1/2