lim_(x->1)(x-3)/(x^2+2x-4) = (lim_(x->1)(x-3))/(lim_(x->1)(x^2+2x-4)
True. Why? The bottom limit is not equal to zero so you can use the quotient rule for separating limits.
lim_(x->2)6
6. Why? the limit of any constant function is just that value
False. Why? f(c) could be a hole, in which case the limit will still exist.
lim_(x->oo)(2x^2-4x+8x^3)/(3x^3-5x^2+7)
8/3. Why? Because both numerator and denominator are degree 3, so to find the horizontal asymptote (since x approaches infinity) we divide the coefficient of each leading term and get 8/3.
If
lim_(x->6)f(x)g(x)
exists, then the limit must be f(6)g(6)
False. Why? one of the functions could have a hole at x = 6. the limits would still exist.
If p is a polynomial, then
lim_(x->b)p(x) = p(b)
True. Why? Because since p is a polynomial, then it is continuous and you can evaluate the limit by substitution
lim_(x->0)(3x^5+12x^2)/(5x^4+6x^2)
2. Why? factor and cancel x2 from numerator and denominator. the resulting simplified function can be used with substitution
True or False: If f(1)>0 and f(3)<0, then there exists a number c between 1 and 3 such that f(c) = 0.
False. Why? We don't know if f is continuous or not.
lim_(x->-oo)(x^2-4)/(x-2)
- oo. Why? Comparing degrees lets us know there is no horizontal asymptote because degree of numerator is larger than degree of denominator. factor and cancel to get x + 2. Imagine that graph and realize that as x -> -oo so does the graph of y = x+2
If
lim_(x->5)f(x) = 0
and
lim_(x->5)g(x) = 0
, then
lim_(x->5)[(f(x))/(g(x))]
does not exist.
False. Why? 0/0 could indicate a hole. So the limit doesn't necessarily not exist.
If
lim_(x->c)f(x) = L
, then f(c) = L
False. Why? There could be a hole at f(c). The limit still exists even though the function value does not.
Calculate
lim_(x->2^-) (f(x))/(g(x))
-sqrt(2)/4
Why? Quotient rule splits into 2 limits.
lim_(x->2^-)f(x) = -1
and
lim_(x->2^-)g(x) = sqrt8 = 2sqrt2
therefore
lim_(x->2^-)(f(x))/(g(x)) = -1/(2sqrt2) = -sqrt(2)/4
Why is this function not continuous?
The more official your answer, the more points you get.
1) the limit of g(x) as x approaches 2 does not exist.
2) the limit of g(x) as x approaches 2 does not equal g(2)
lim_(x->3^-)(4-3x)/(x-3)
Infinity. Why? Since x = 3 is a vertical asymptote of the function, the limit should approach either infinity or negative infinity. Plug in something close to 3 from the left side (x = 2.9 works) and analyze the signs of the function. Both numerator and denominator would be negative when you plug in 2.9 so the limit approaches positive infinity.
if
lim_(x->5)f(x) = oo
and
lim_(x->5)g(x) = oo
, then
lim_(x->5)[f(x) - g(x)] = 0
False. Why? infinity isn't exactly a set number. There are different sizes of infinity so doing infinity - infinity isn't necessarily equal to zero.
If f is continuous at 5 and f(5) = 2 and f(4) = 3, then
lim_(x->2)f(4x^2-11) = 2
True. Why? 4x2 - 11 is continuous so can plug in x = 2 to get y = 5. f is continuous at x = 5 so can plug in f(5) to get 2. the fact that f(4) = 3 is totally irrelevant.
Use one sided limits to explain why the limit as x approaches 2 not exist for this function
Let f be the function that is continuous on the closed interval [3,5] with f(3) = 9 and f(5) = 22. Which of the following is guaranteed by IVF?
A) f(x) = 11 has at least one solution in the open interval (3,5)
lim_(x->-oo)(5-3x)/(sqrt(x^2+3))
3. Why? because
(5-3x)/(sqrt(x^2+3)) = (5/(-x)-(3x)/(-x))/(sqrt(x^2/(x^2)+3/(x^2))) = (-5/x+3)/sqrt(1+3/x^2)
lim_(x->4)((2x)/(x-4)-8/(x-4)) = lim_(x->4) (2x)/(x-4) - lim_(x->4)8/(x-4)
False. Why?
lim_(x->4)((2x)/(x-4)-8/(x-4))
can be simplified/factor and cancel to get 2 but if the limits are separated, then each of those does not exist. 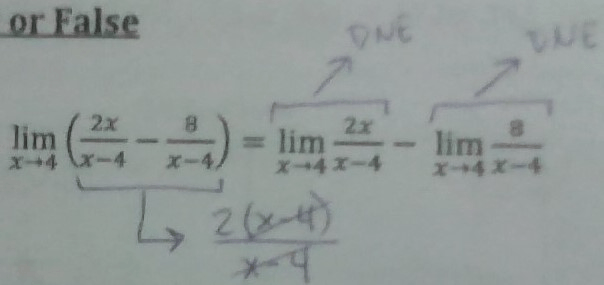
If
lim_(x->5)f(x) = 2
and
lim_(x->5)g(x) = 0
, then
lim_(x->5)(f(x))/(g(x))
does not exist
True. Why? because a number divided by zero indicates that there is a vertical asymptote at that x value.
If f(x) = 3x2 + 4x, then find
lim_(h->0)(f(x+h)-f(x))/h
6x+4. Why? 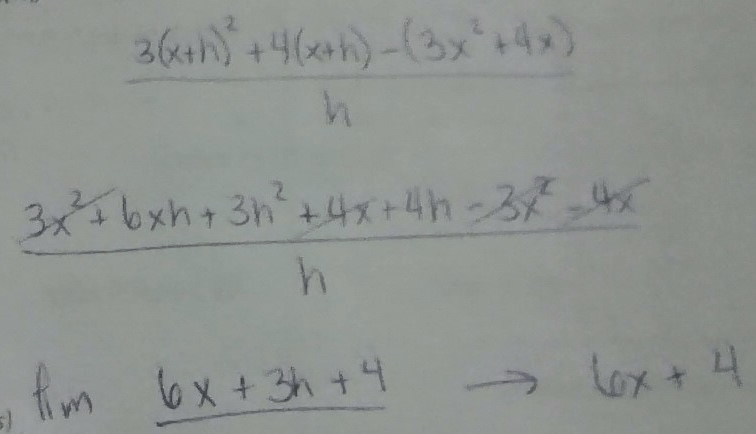
Find values of k and m so that the function is continuous for all real numbers.
k = -7 and m = 1/2.
How? set the first two equations equal at x = -2 and the bottom two equations equal at x = 3.
lim_(x->oo) cosx
DNE. Why? because cosx keeps going between -1 and 1. It does not approach one single value.
False. Why? if f(x) is a piecewise function you could get a vertical asymptote from one side (by definition, VA's only have to exist from one side). a second piece of the function could start on the first piece's vertical asymptote