What is the left and right end behavior of
(2x^2-5x)/(4+3x^2)
lim_(x->-oo)=2/3
lim_(x->oo)=2/3
Where does this graph have a vertical asymptote?
2/(3x^2)
x=0
Solve the inequality
(x-4)/(x+1)<0
(-1,4)
What is the domain of this graph?
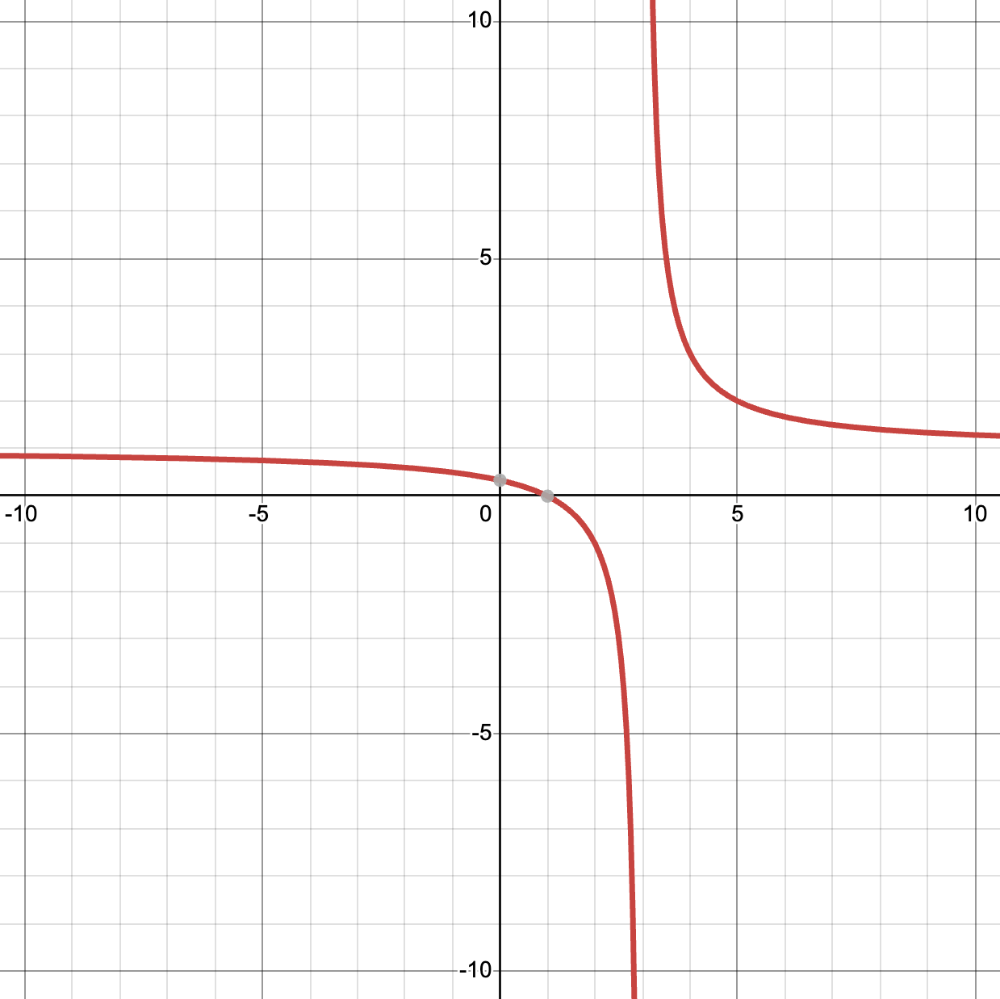
(-oo,3)U(3,oo)
Find the 2rd term of
(3x-5)^4
-540x3
What is the left and right end behavior of
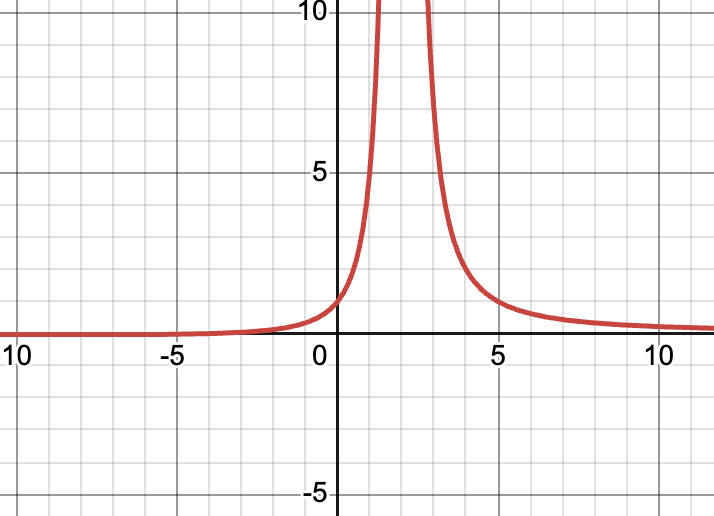
lim_(x->-oo)=0
lim_(x->oo)=0
Where does this graph have a hole?
(x^3-7x)/(x^2-4x)
(0,7/4)
((x+3)(x-1))/(x-4)>=0
[-3,1]U(4,oo)
What is the range of this graph?
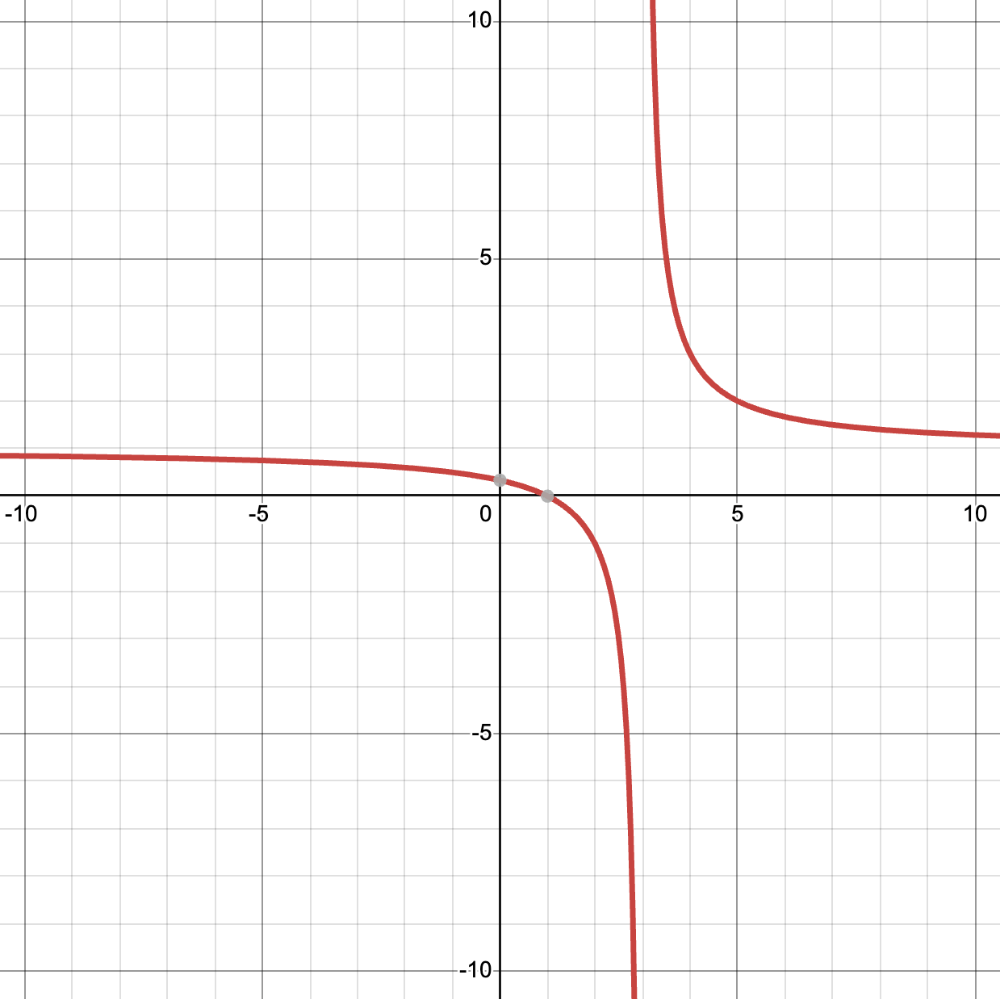
(-oo,1)U(1,oo)
Find the transformations of:
(4x+1)/(x-2)
Vertical translation: 4
Vertical dilation: 9
Horizontal translation: 2
What is the limit statement describing the output values when the input values decrease without bound?
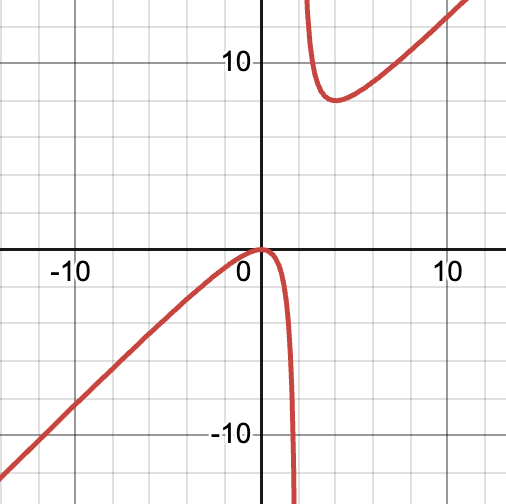
lim_(x->-oo)=-oo
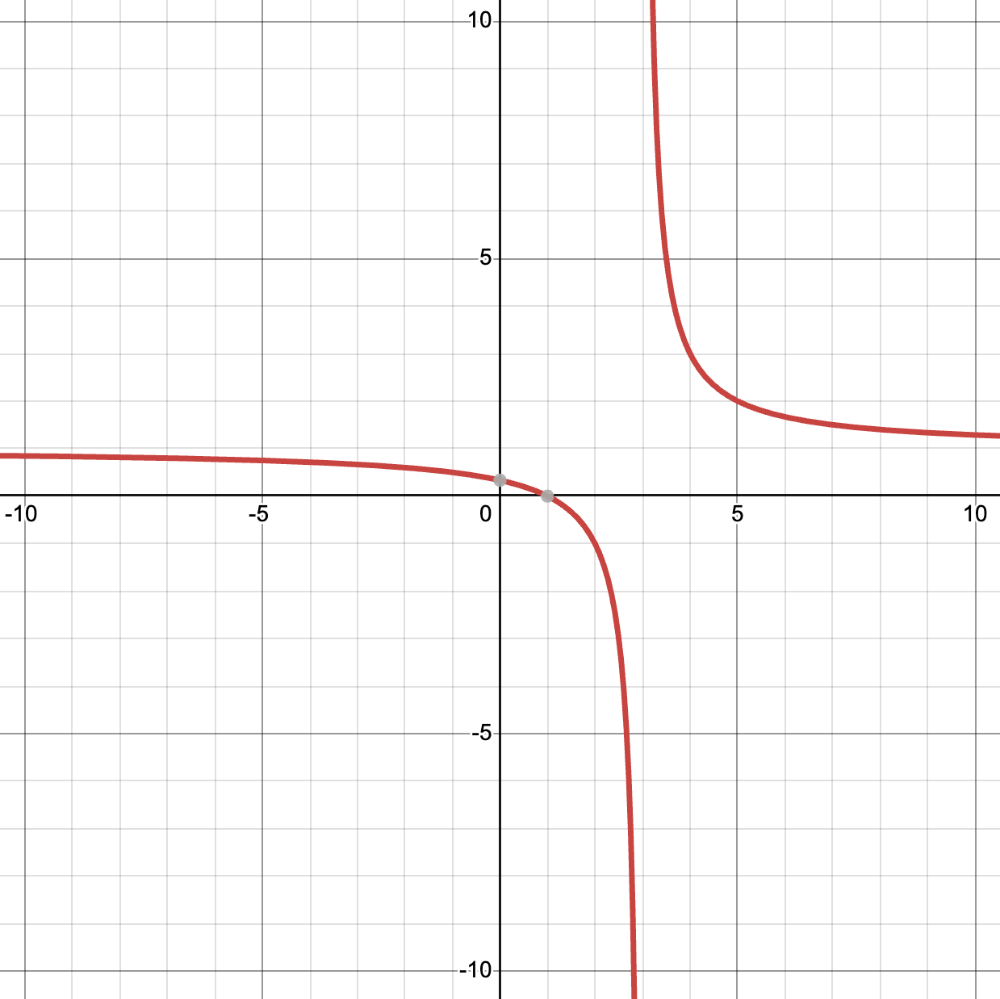
lim_(x->3-)=
-oo
((x+3)^2(x-1))/(x-4)<=0
[-3]U[1,4)
What is the domain of:
((x-5)(x+1))/((x+1)(x+3))
(-oo,-3)U(-3,-1)U(-1,oo)
Find the 3rd term of
(2x-3)^5
720x3
What is the left limit statement for
((x-2)(x+3))/((x-2)(x+1))
lim_(x->-oo)=1
lim_(x->3-)=0
lim_(x->3+)=0
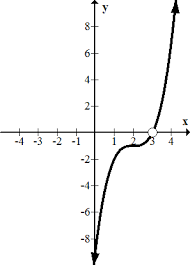
lim_(x->3-)=0
lim_(x->3+)=0
((x+2)(x-5))/(x-1)^2<0
(-2,1)U(1,5)
What is the range for:
(2x^2-5x+1)/(x^2)
(-oo,2)U(2,oo)
Is the data linear, quadratic, or neither?
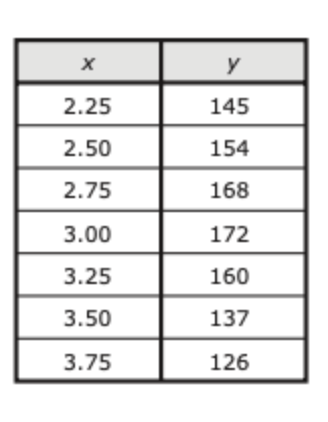
Quadratic
What is the right end limit statement for
(x^3-2x^2+8)/(-4x^2)
lim_(x->oo)=-oo
lim_(x->2-)=
((x-2)(x+1))/((x-3)(x-2))
lim_(x->2-)=-3
When are two times do we not include the points in our answer?
1. Vertical Asymptote
2. Hole
3. When it's > or < instead of "or equal to"
What is the domain for:
(x^3-x^2-12x)/x^2
(-oo,0)U(0,oo)
Find a quadratic equation for this data (round to the nearest hundredth)
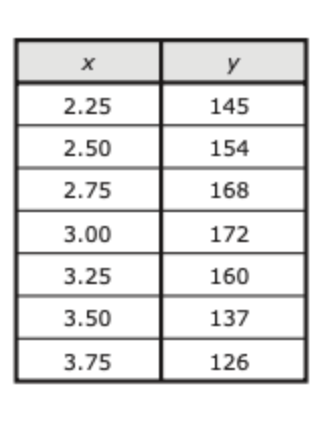
-60.38x^2+348.14x-334.19