Equations
Transformations
Parametric Equations and Inverse Functions
Functions
Word Problems
100
Solve 2x2 - 6 = x
X= 2, -3/2
100
Draw the graph of y=(x-3)²
100
Find ordered pairs in the relation x(t)= t2-2 and y(t)= 3t for t= -2, 1, 5
t(-2) = (2, -6)
t(1) = (-1, 3)
t(5)= (23, 15)
100
Find (f+g), (f-g), (fg) as expressions in x
f(x)=3x+5, g(x)=x2
(f+g)(x)=x2+3x+5, (f-g)(x)=3x+5-x2, (fg)(x)=x2(3x+5)
100
An auto parts store wants to lease a 50-ton punch press. There are 2 leasing plans. Plan 1 is a flat fee of $25,000 plus a charge of $2,000 per month. Plan 2 is a $2,000 flat fee with a monthly charge of $3,800. When is plan 1 less expensive that plan 2?
After 12.8 months
200
Solve Alegebraically.
|x+3| = 2x-4
X = 7, 1/3
200
Describe the transformations from the graph of y=x² to y=(x+5)² - 3
left 5, down 3
200
Determine whether the ordered pair is in the relation
x_2y2=1 a. (3,-1) b. (-1,1)
a. Yes
b. No
200
Find f(g(x)) and its domain
f(x)=x2-3, g(x)=1/x+2
f(g(x))=[1/(x+2)2]-3
Domain=(-infinity, -2) U (-2,infinity)
200
A person who is 5 feet tall is standing next to a streetlight that is 12 feet tall at night time. The person walks 4ps away from the light. Find the length of the person's shadow 7 seconds after they start walking.
x=20
300
Solve Graphically
√x + 3 > √4 - x
(1/2, 4]
x > .5
300
Give the equation for h(x):
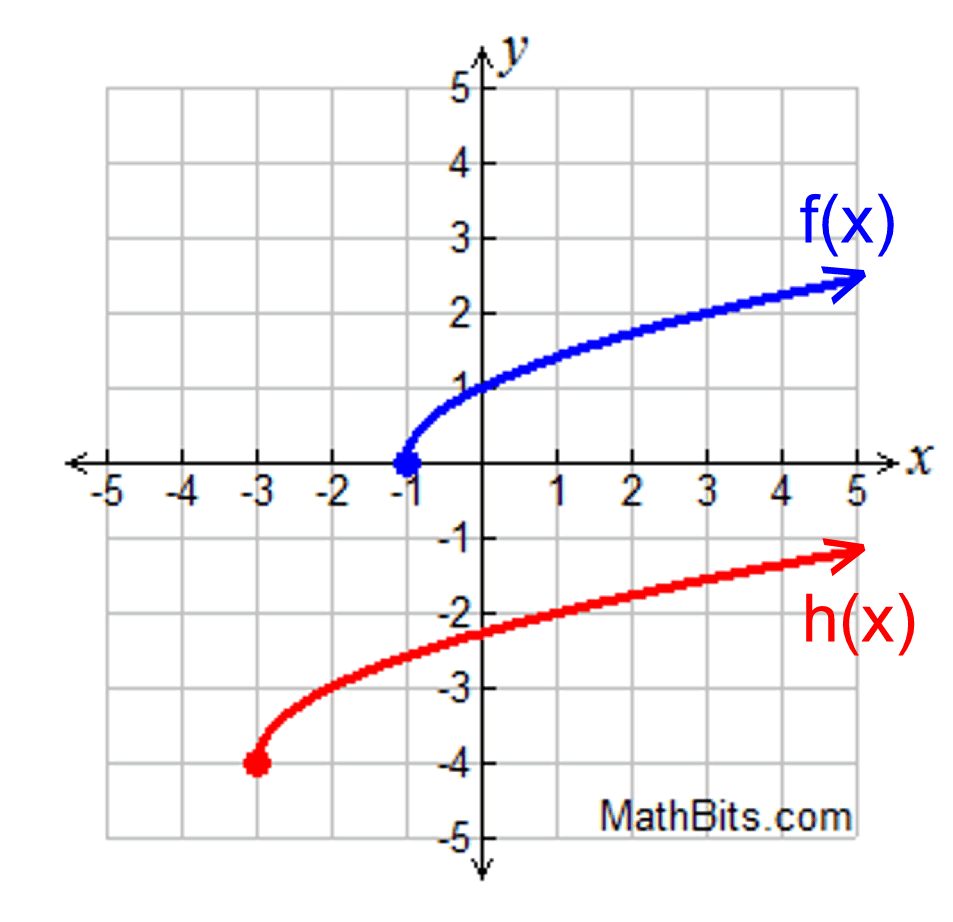
h(x)=(√x+3)-4
300
Determine whether the ordered pair is a part of the relation
x2+y2<4 a. (square root of 2, square root of 2) b. (1,1.5)
a. No
b. Yes
300
Find f(x) and g(x) so that the given function can be written as y=f(g(x))
y=|x2+x|
f(x)+|x|, g(x)=x2+x
300
2 airplans leave detroit at the same time. The Boeing 747 flies east at a constant speed, and the DC9 flies south at a constant speed. The Boeing 747 flies 50 mph faster than the DC9. After 1.5 hours the planes are 870 miles apart. How fast is each plane flying?
DC9: 384.359 mph
Boeing 747: 434.359 mph
400
Solve completing the square
4x2 -20x + 17 = 0
X = 5/2 +/- √2
400
Find the equation y2 when y1=x² and the transformations to get y2 are a vertical stretch by a factor of 2, and a shift to the right 3 units
y2=2(x-3)²
400
Find the inverse for y=x³-5
y=(∛x+5)
400
Find f(x) and g(x) so that the given function could be written as y=f(g(x))
y=2/(x+3)2
f(x)=2/x, g(x)=(x+3)2
400
A relief agent drops food containers from an airplane on a war-torn famine area. The drop was made from an alitutde of 1,000 ft above ground level.
a) Use an equation to model the height of the containers (during free fall) as a function of time t.
b) After 4 seconds of free fall, parachutes open. How many feet above the ground are the food containers when the parachutes open.
a) y= -16t2 + 1000
c) when t =4 y= 744ft
500
Find discriminant and #/type of solutions and graph
9x2 +42x+49=0
D=0
1 real solution
double root
500
Describe the transformations of the function f(x)=∛x to h(x)=-3(∛x-4)-2
4 units right, vertical stretch by a factor of 3, reflect over x axis, and 2 units down
500
Determine if f(x) and g(x) are inverses by finding f(g(x)) and g(f(x))
f(x)=2x+5
g(x)=½(x-5)
Yes, they are inverses
500
Find f(g(2)) and g(f(2))
f(x)-x3 -1, g(x)=x+3
f(g(2))=124 and g(f(2))=10
500
Two airplanes leave Wichitia at the same time. The Airbus flies due North toward Winnipeg, and the Turbo Prop flies due east toward Raleigh. The two airplanes fly at a constant rate, and the Airbus flies 55 mph less than twice as fast as the Turbo Prop. After 1.5 hours they are 765 mi apart. How fast is each of the two airplanes flying?
Turbo Prop: 249.8 mph
Airbus: 444.6 mph