An object speeds up from rest and moves 10 m in the first 2 s. How far does the object move in the first 6 s?
90 m (triple the time, nonuple the distance)
Consider the p-t graph below. Is this object (a) speeding up, slowing down, or moving at a constant speed? (b) What direction is the object moving?

(a) constant speed (constant slope - it's a p-t graph!)
(b) moving in the positive direction
An object was dropped from rest. How fast is it going after 3.2 seconds?
vf = vi + g*t
vf = 0 + (10 m/s/s)*(3.2 s)
vf = 32 m/s downwards
An object has an initial velocity of 36 m/s south. if the object accelerates north at 5m/s2 for 2s, what will be the final velocity of the object? (clearly state magnitude AND direction)
vf = 26 m/s south
Students are drawing a motion map of an object speeding up from rest with constant acceleration. They draw the first two dots correctly (the two solid red circles shown below). They are trying to decide where to put the next dot. Which location, A, B, or C, shows the correctly location of the next dot?

Dot C

Velocity and time information for a rightward-moving car are shown. Determine the magnitude and direction of the car's acceleration.
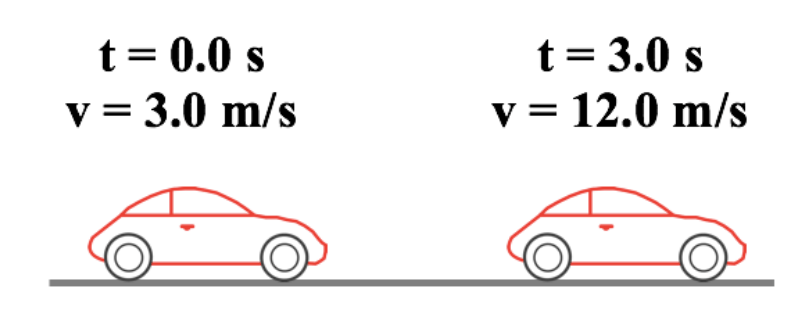
a = (Delta v) / (Delta t)
a = (vf - vi) / (tf - ti)
a = (12.0 m/s - 3.0 m/s) / (3.0 s - 0.0 s)
a = (9.0 m/s) / (3.0 s)
a = 3.0 m/s/s
An object was tossed directly upwards. What is the object's (a) velocity and (b) acceleration at its peak?
(b) acceleration = 10 m/s/s downwards
An airplane accelerates down a runway at 3.20 m/s2 for 32.8 s until is finally lifts off the ground. Determine the distance traveled before takeoff.
d = 1720 m
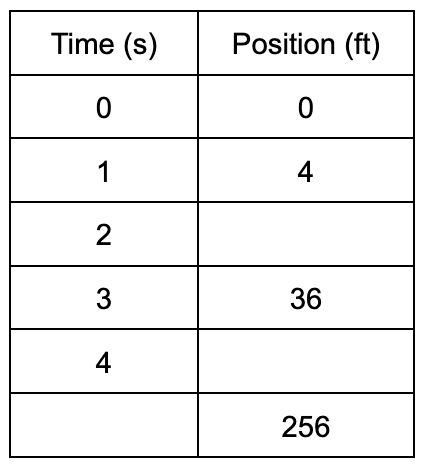
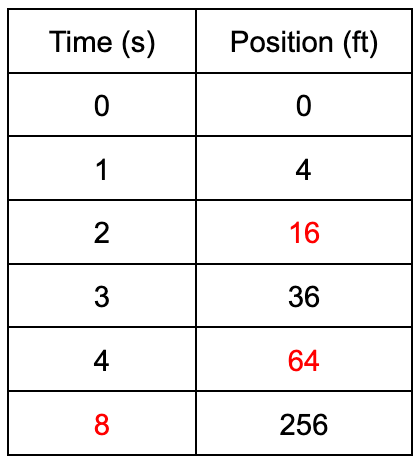
A skateboarder accelerates from rest down a hill. Fill in the blanks in the following p-t data:
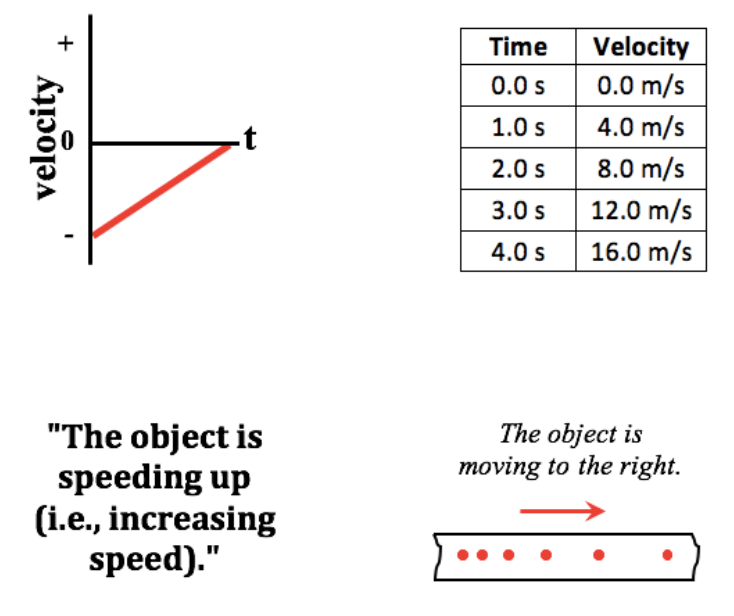
One of these representations is not like the others. Which one? Right is + and left is -.
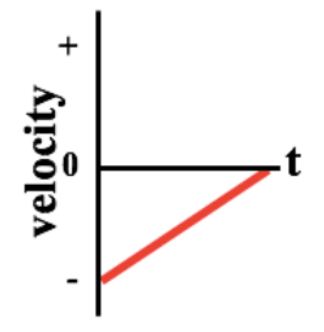
Draw a p-t graph and matching v-t graph that are impossible to result from free-fall motion. Let's call up + and down -.
Impossible in free fall: Any matching graph pair that shows...
... moving downwards while slowing down.
... moving upwards and speeding up.
... constant velocity motion.
A kangaroo is capable of jumping to a height of 2.62 m. What equation would you use to determine the takeoff speed of the kangaroo?
vf2 = vi2 + 2*a*(Delta x)
The time-independent equation.