No obtuse triangles are also isosceles.
False
Any two angles, adjacent or otherwise, that add to equal two right angles are called _________.
Supplementary
In triangle CAB, m<A > m<C. If AB=25 and BC= 3y + (7-2y).
What inequality must we set up to solve this?
BC> AB
G: ABC is isosceles, with legs AB and AC. AD bisects <BAC.
TP: < ADB is right
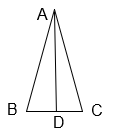
What information do we know because the triangle given is isosceles (by its definition)?
AB = AC
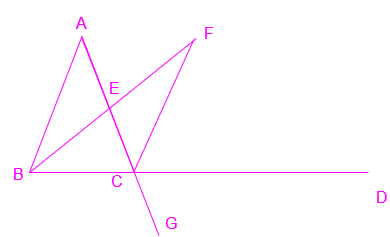
Enunciation: If two straight lines cut one another, they make the vertical angles equal to one another.
What is the given of this proposition?
AB and CD intersecting at E.
The converse of a statement may in some cases only be able to be proved indirectly.
True
Any two angles, adjacent or otherwise, that add to equal one right angle are called _______.
Complimentary
In triangle CAB, m<A > m<C. If AB=25 and BC= 3y + (7-2y).
What proposition do we learn the information needed to solve the last question?
I.19
G: ABC is isosceles, with legs AB and AC. AD bisects <BAC.
TP: < ADB is right

What information do we know because the triangle given is isosceles (from a proposition)?
<ABD = < ACD
Enunciation: If two straight lines cut one another, they make the vertical angles equal to one another.
What is the to prove of this proposition?
<AED = <CEB and <AEC = <DEB
Given any three line segments, with a straight edge and a compass a triangle can be constructed with sides equal in length to the given three segments.
False
Any two lines which meet make ________________ angles equal.
Vertical
In triangle CAB, m<A > m<C. If AB=25 and BC= 3y + (7-2y).
What are the possible values of y?
y>18
G: ABC is isosceles, with legs AB and AC. AD bisects <BAC.
TP: < ADB is right

What information do we know because <BAC is bisected ?
< BAD = <CAD
Enunciation: In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.
What is the given of this proposition?
Triangle ABC, side BC extended to D.
There are only four valid methods for proving triangles congruent in general, although in special cases other methods may be found.
True
If the two sides of two adjacent angles which are not shared fall in a straight line, the angles are called a __________________ _____________.
Linear Pair
In triangle CAT, CA=12, AT= x+5 and CT=2x-7.
What inequality do we need to solve for x?
CA + AT > CT
CA + CT > AT
AT + CT > CA
G: ABC is isosceles, with legs AB and AC. AD bisects <BAC.
TP: < ADB is right

By what congruence theorem are triangles BAD and ACD proven congruent?
ASA
Enunciation: In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.
What is the to prove of this proposition?
<ACD > <ABC
<ACD > <BAC
In any triangle, the difference in lengths of 2 sides is always greater than the third side.
False
The sum is always greater.
If two lines are _____________________, then they create adjacent angles which are equal.
perpendicular
In triangle CAT, CA=12, AT= x+5 and CT=2x-7.
What are the possible values of x?
(14/3) < x < 24
G: ABC is isosceles, with legs AB and AC. AD bisects <BAC.
TP: < ADB is right

Since triangle BAD and CAD have been proven congruent, how do we know <ADB is right?
<ADB = <ADC [CPCTC]
<ADB is right [Definition of a right angle]
Enunciation: In any triangle, if one of the sides be produced, the exterior angle is greater than either of the interior and opposite angles.
What is the diagram of this proposition?