Vocabulary
Writing Linear Functions
Graphing Linear Functions
Slope
Intercepts
Modeling with Linear Functions
100
Slope
the steepness of a line
100
Write a linear function with a slope of -9 and a y-intercept of 5
y =-9x+5
100
Which list contain points that lie on the graph of
y = 2x − 1?
a. (0, -1), (15, 29)
b. (-2, -4), (1, 3)
c. (-2, -3), (0, 0)
d. (2000, 1999), (3, 5)
a. (0, -1), (15, 29)
100
Identify the slope of the linear equation
y = -x + 6
The slope is -1
100
What are the x and y-intercepts of the following graph?
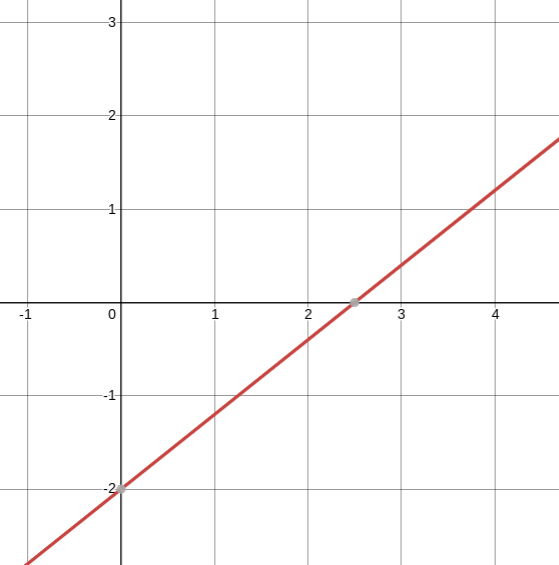
x-intercept: 2.5
y-intercept: -2
100
What are the two forms we have learned to write a linear equation?
Slope Intercept form
Standard form
200
x-intercept and y-intercept
The x intercept is the point where the line crosses the x axis. At this point y = 0.
The y intercept is the point where the line crosses the y axis. At this point x=0
200
Write the linear function in this graph:
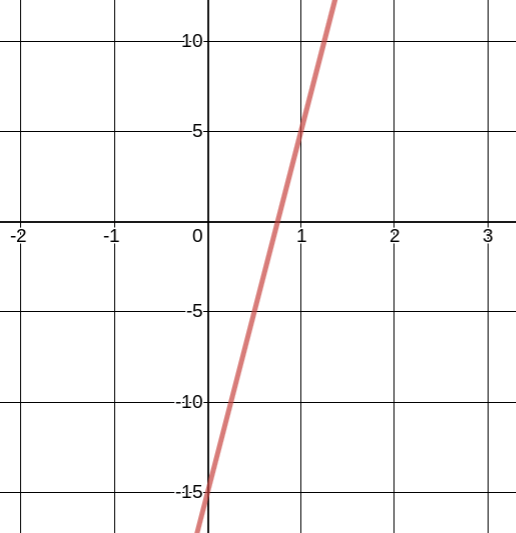
y=20x-15
200
Find the slope of a line that passes through the points (0, 5) and (2, 10)
m = 5/2
200
What are the x and y-intercepts of the linear function:
4x+2y=8
x-intercept: 2
y-intercept: 4
200
Anthony is buying carrots and celery at the grocery store. The carrots cost $1.50 per pound, x. The celery costs $1.25 per pound, y. He has a total of $10 to spend.
Write an equation in standard form that represents how many pounds of carrots x and pound of celery y that he can buy.
1.5x+1.25y=10
300
Function
A function is an equation that turns a given input into an ouput
300
3x-2y=10
y=3/2x-5
300
What is the slope of the linear function
y = 14
0
300
What are the x and y-intercepts of the linear function
12x – 6y = –36
x-intercept:(-3,0)
y-intercept: (0,6)
300
Maria wants to buy oranges and bananas at the store. Let x represent the number of oranges and y represent the number of bananas. Oranges are $5 a pound and bananas are $4 a pound. She has a total of $20 to spend.
Write an equation in standard form that represents the situation.
5x+4y=20
400
Point on a Line
An ordered pair that is a solution to a linear function
400
Write a linear function that contains the points (0,2) and (-4,5).
y =3/4x +2
400
Would (2,-2) be a solution to the inequality
y ≤ 2x + 1?
Yes because if (2, -2), then
-2 ≤ 2(2) + 1
-2 ≤ 4 + 1
-2 ≤ 5
Since this is true, (2,-2) is a solution.
400
Find the slope of a linear function that contains the points (-2.5 , 9) and (5 , -13.5)
m=(-13.5-9)/(5-(-2.5))=-22.5/7.5
m=-3
400
What are the x and y-intercepts of the linear function:
-10x + 6y = -30
x-intercept: 3
y-intercept: -5
400
T-Mobile charges $100 a month for a family plan for four people. They also charge a one time set up fee of $25. Write a function to show how much money she spends in total after x months.
y=100x+25
500
What does it mean for a function to be linear?
For every one increase in the input, the output increases/decreases at a constant rate
500
Describe how we would graph the linear function:
-8x + 4y = 12
First, find the x-intercept and the y-intercept. Next, graph the two points on the x-axis and y-axis. Lastly, connect the points and use the rise/run to graph more points if necessary.
500
Write the equation of the table below.
x -1 2 5 8
y -2 7 16 25
y = 3x + 1
500
Identify the slope and y-intercept of the standard form equation
-5x + 3y = -15
Slope intercept form y = (5/3)x - 5
Slope: 5/3
y-intercept: -5
500
You are at school, 12 miles away from home. You start walking home with your friends at a speed of 3 miles per hour towards your home.
a. Write an equation that represents your distance from home (y) after (x) hours.
b. What does the slope of the equation represent?
c. What does the y-intercept of the equation represent?
a. y = -3x + 12
b. 3 miles per hour - walking closer to home (it is negative since the distance is getting shorter)
c. 12 miles away from home (the starting point)