 The relationship between angle 1 and angle 3
The relationship between angle 1 and angle 3
What is vertical angles?
The value of angle b.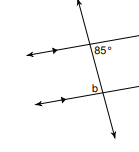
What is 85 degrees?
The value of x.
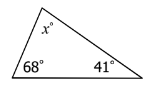
What is x=71.
What is the formula for the sum of the interior angles of a polygon?
What is (n-2)*180?
To prove two triangles are similar, we need to show that at least__________sets of angles are congruent.
What is 2?
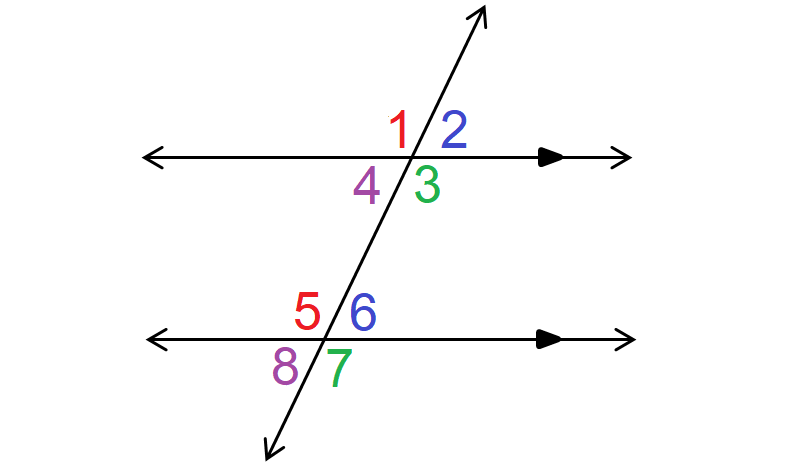
The relationship between angle 2 and angle 6.
What is corresponding angles?
The value of the missing angle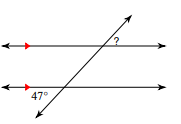
What is 47 degrees?
The value of the exterior angle.
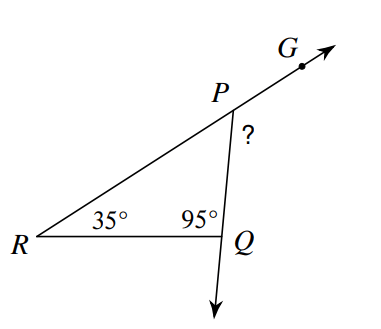
What is 130 degrees?
In the formula (n-2)*180, n-2 represents ...
What is the number of triangles inside the polygon?
Similar or not similar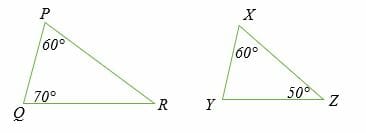
What is similar?
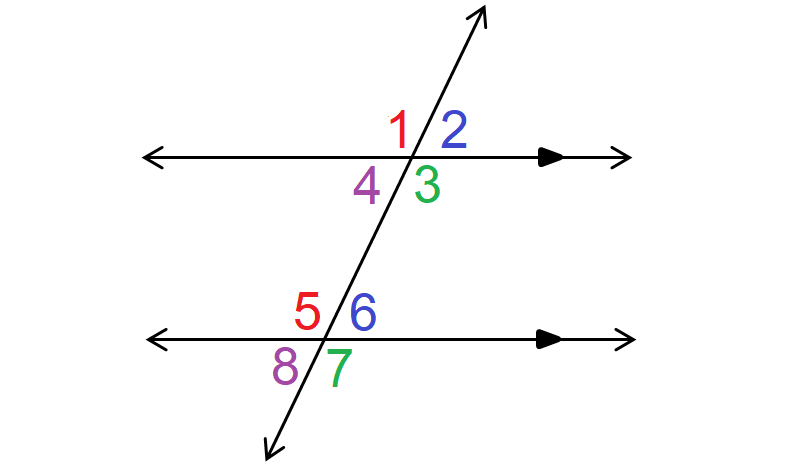 The angle relationship between angle 3 and angle 5.
The angle relationship between angle 3 and angle 5.
What is Alternate Interior Angles?
The value of the missing angle
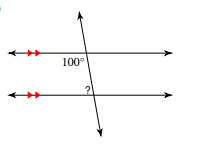
What is 80 degrees?
The value of x.
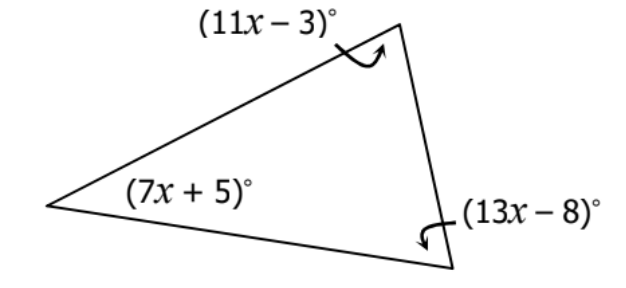
What is x=6?
The sum of the interior angles is...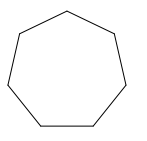
The triangles are similar because
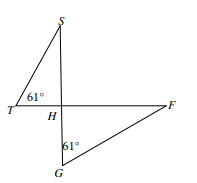
What is vertical angles claims the second set of congruent angles?
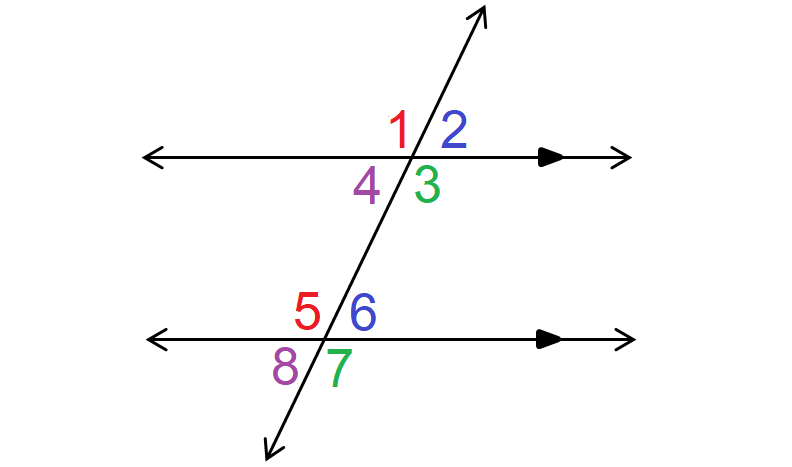 The angle relationship between angle 2 and angle 8.
The angle relationship between angle 2 and angle 8.
What is Alternate Exterior Angles?
Solve for x.
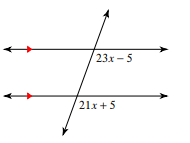
What is x=5
The value of x
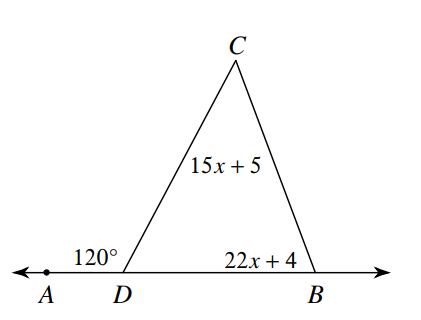
What is x=3?
The sum of the interior angles is...
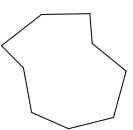
What is 1260 degrees?
Explain if the triangles are similar?
What is no since there is only one set of congruent angles?
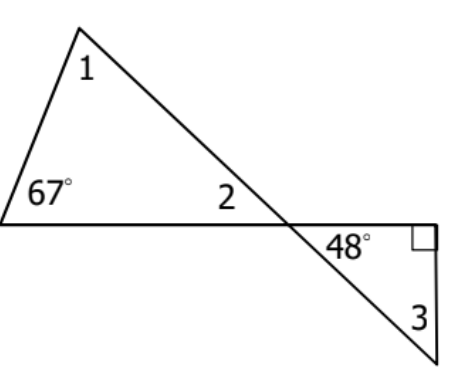
Angle 1: 65 degrees
Angle 2: 48 degrees (vertical angles)
Angle 3: 42 degrees
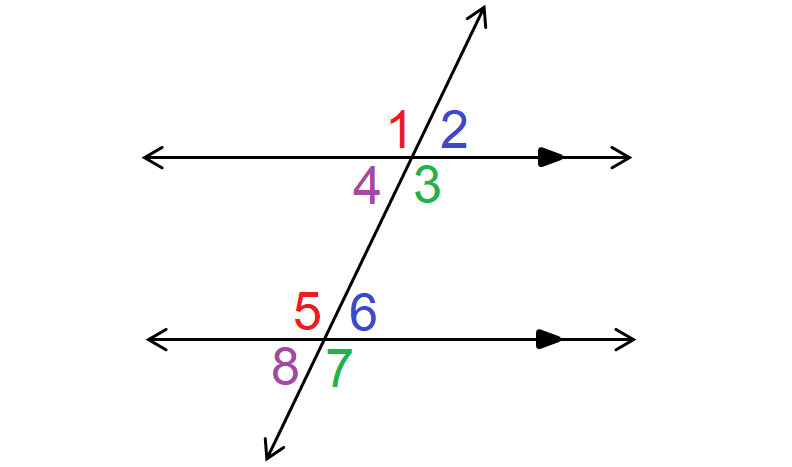 The angle relationship between angle 6 and angle 7.
The angle relationship between angle 6 and angle 7.
What is Supplementary Angles?
The value of x
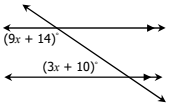
What is x=13
The value of Angle B.
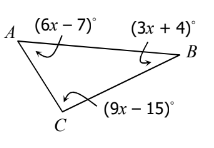
What is 37 degrees?
The image below is a regular polygon. The measure of one of the angles is...
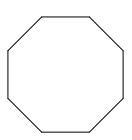
What is 135 degrees.
Explain how the triangles are similar
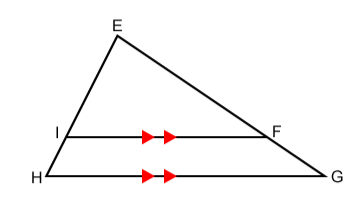
What is two sets of congruent angles? (Angle Angle)
Angle E is congruent to itself. We can use corresponding angles to find the second pair of congruent angles.