Quadratics General
Standard Form
Vertex Form
100
State if the following are quadratics are in standard form or vertex form: y=3x2+2x-1, y=x2-4x, y=-(x+4)2 + 5, and y = (x-7)2
3x2+2x-1 and x2-4x are in standard form and -(x+4)2+5 and (x-7)2 are in vertex form
100
Write in standard form y=(x-6)2+12
What is y=x2 - 12x + 48
100
Find the vertex of y=3(x-4)2 - 7 and describe the transformations.
What is (4,-7). Transformations are Right 4, Down 7, and Vertical Stretch
200
Find the axis of symmetry, vertex, zeros, and determine the max or min value.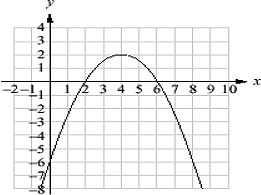 
What is AOS: x=4, Vertex: (4,2), Zeros (2,0)(6,0) and the quadratic is a max with a value of 2
200
Find the axis of symmetry for y = x2 - 8x + 10
What is AOS x=4
200
Find the vertex and Graph y = -2(x-3)2 + 6
300
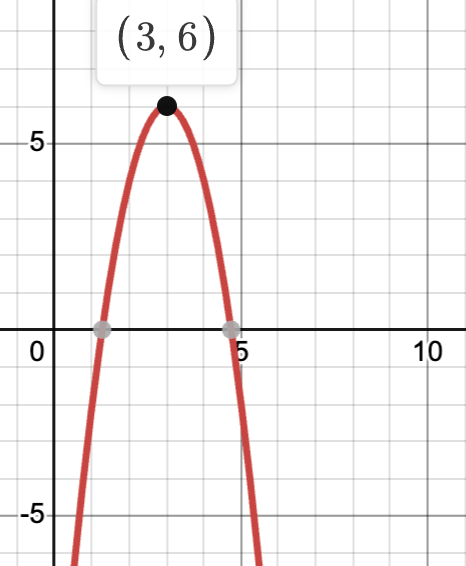
Find the domain and range
What is Domain: -∞ < x < ∞ or (-∞,∞) or All Real Numbers, Range: y≤2 or (-∞,2]
300
Find the axis of symmetry, vertex, and determine if it is a max or min. y = x2 - 2x - 5
What is AOS x=1, Vertex (1,-6), and the quadratic is a min
300
What is the AOS, Domain, Range, and Zeros of the following graph?
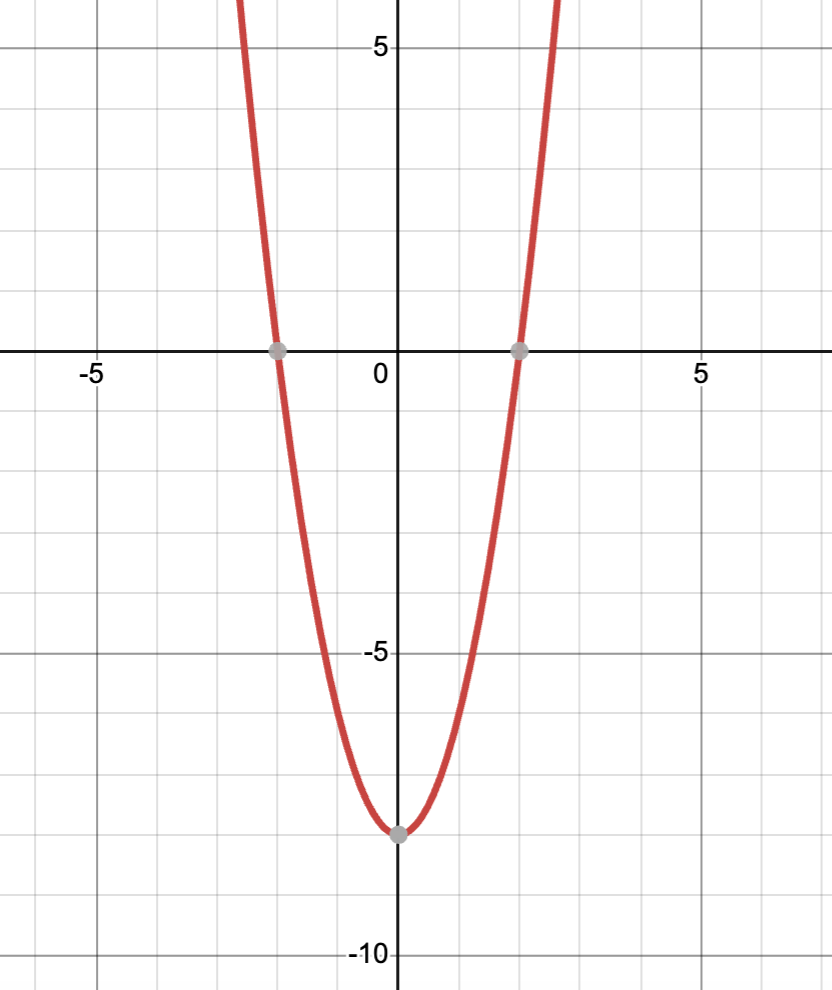
AOS: x=0, Domain: (-∞,∞), Range: [-8,∞), Zeros: (-2,0)(2,0)
400
What are the x intercepts of the quadratic:
y=(x-2)2 - 9
(5,0)
(-1,0)
400
What is the vertex of y = x2+4x+3
Vertex = (-2,-1)
400
Find the vertex, AOS, and max or min value of y=-2(x+3)2 + 7
Vertex (-3,7), AOS: x=-3, Max Value of 7.
500
Find the domain and range of y=x2 - 5
What is Range: y≥-5 or [-5,∞). The Domain (-∞,∞) or -∞<x<∞
500
What is the axis of symmetry and vertex
y = x2 - 6x + 4
AOS: x=3
Vertex: (3,-5)
500
What is the y-intercept:
y= - 2(x-1)2+12
Y-intercept (0,10)