Random
Addition and Subtraction
Matrix Multiplication
Inverses
Systems of Equations
100
What the the order of the matrix
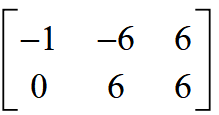
2x3
100
What is the rule for determining if two matrices can be added or subtracted together?
The matrices have to be the exact same dimensions (equal number of rows and columns)
100
If you are able, how do you multiply matrices?
You multiply each row in the first matrix by each column in the second matrix.
BONUS (+100): You multiply the corresponding elements and then add each of those products together to get each individual element in the solution matrix.
100
How do you know if a matrix does not have an inverse?
If the determinant equals zero.
100
What are the two methods to solve a system of equations using matrices?
Cramer's Rule and Inverses
200
Identify element a23 from A =
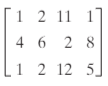
2
200
Find A - B:
A = [[2,-3],[-1,4]]
B=[[-4,1],[3,-2]]
A-B=[[-6,4],[4,-6]]
200
Multiply A and B.
A=[[1,1],[1,1]]
B=[[0,3],[4,4]]
AB=[[4,7],[4,7]]
200
Determine if these two matrices are inverses:
A=[[-9,-4],[-5,-2]]
B=[[1,-2],[-5/2,9/2]]
Yes, they are!
200
Solve using Cramer's Rule:
-4x - 7y = 2
5x - y = 7
x=47/39 and y=-38/39
300
Identify
1. 2x2 identity matrix
2. 3x3 identity matrix
1. [[1,0],[0,1]]
2.[[1,0,0],[0,1,0],[0,0,1]]
300
Find B - A
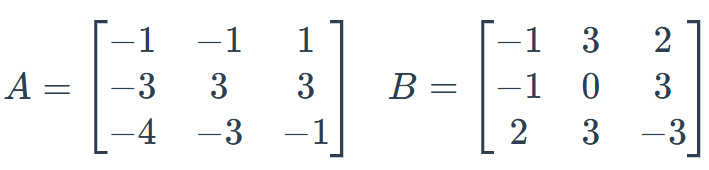
[[0,4,1],[2,-3,0],[6,6,-2]]
300
Multiply:
[[1,2, -2, -1],[-3, -4, 4, 3]] [[5],[6],[7],[8]]
[[-5],[13]]
300
If possible, find the inverse of A:
A=[[3, 3],[-1, -1]]
A does not have an inverse.
300
Solve using matrix inverses:
6x - 3y = -1
8x - 5y = -2
x=1/6 and y=2/3
400
A group of friends is playing a Rock-Paper-Scissors Tournament. For each win they get 5 points and for a draw they get 2 points. Using matrices, determine the winner and by how many points they won.
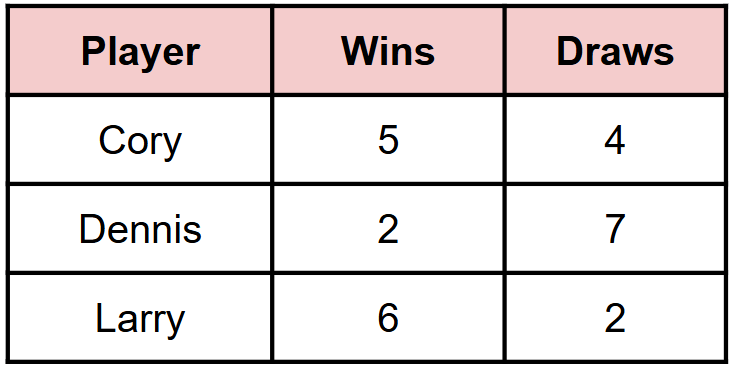
Larry won by 1 point!
400
Find -1/3 B + 3A
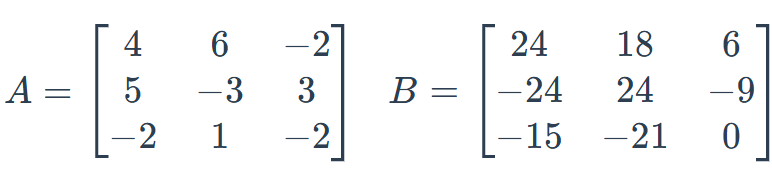
[[4,12,-8],[23,-17,12],[-1,10,-6]]
400
Multiply:
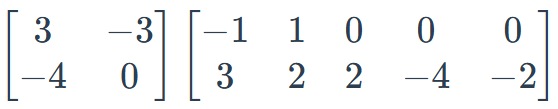
[[-12,-3,-6,12,6],[4,-4,0,0,0]]
400
If possible, find the inverse of A:
A=[[2,6],[-1,-5]]
A^-1=[[5/4,3/2],[-1/4,-1/2]]
400
Solve using matrix inverses:
3x + 4y = 10
-3x - 7y = -5
x=50/9 and y=-5/3
500
Can the following matrices be multiplied together? How do you know? If so, what would the size of the solution matrix be?
[[1,2],[3, 4],[5, 6]] [[1,2, 3],[4, 5, 6]]
Yes, because the first matrix is a 3x2, and the second matrix is a 2x3. Since the second matrix has the same number of rows, as the first one has columns (2), these matrices can be multiplied together. Their product matrix would have 3 rows and 3 columns.
500
Find -2A - 1/6 B
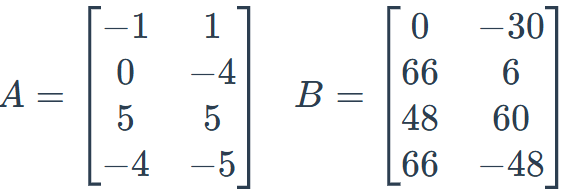
[[2,3],[-11,7],[-18,-20],[-3,18]]
500
Multiply:
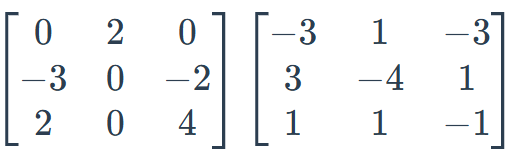
[[6,-8,2],[7,-5,11],[-2,6,-10]]
500
If possible, find the inverse of A:
A=[[3, 4],[-2, -1]]
A^-1=[[-1/5, -4/5],[2/5, 3/5]]
500
Solve using Cramer's Rule:
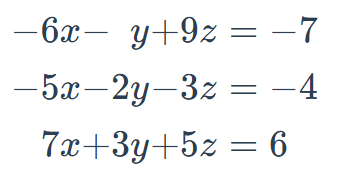
x=-5/7 , y=34/7 , and z=-5/7