Characteristics of graphs
Converting between forms
Average Rate of Change
100
Using the function f(x)=2(x+1)(x+5), and the graph chosen above, determine the following:
1. Range
2. X-Intercepts
3. End Behavior
1. If the parabola has a minimum (facing up), it can be written as y ≥ or [ , ∞) . If the parabola has a maximum (facing down), it can be written as y ≤ or [-∞, ). In this graph of the function f(x)=2(x+1)(x+5), the parabola is facing up and its minimum value is -8 so the range would be y ≥ -8 or [-8, ∞)
2. To find the x-intercepts, we need to factor the function, but this function is already in intercept form so we just need to solve it x + 1 = 0; x + 5 = 0. After solving, we have (-1, 0) and (-5, 0)
3. To find the end behavior we need to look at the end of the left end and right end of the x-axis. Because the graph is going up so we would write it as: as x -> -∞, y -> ∞. as x -> ∞, y -> ∞
100
Which of the following equations is f(x) = 3(x−5)2 − 7 expressed in standard form?
Question options:
f(x) = 3x2 + 30x + 79
f(x) = 3x2 + 30x + 83
f(x) = 9x2 + 42x + 499
f(x) = 3x2 + 30x + 68
To express the equation in standard form we need to simplify it.
3(x2 - 10x + 25) -7
3x2 - 30x + 75 -7
3x2 - 30x + 68
f(x) = 3x2 + 30x + 68 is the answer
100
What is the average rate of change over the interval [0, 2]?
Question options:
-1
-2
-3
-4
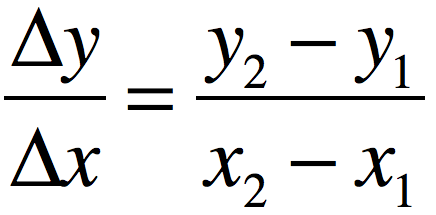
(-4-4) / (2-0) = -8/2 = -4
the average ROC over the interval [0, 2] is -4
200
The equation y=−x2−2x+8 is graphed on the set of axes below.
Based on this graph, what are the roots/zeros of the equation y=−x2−2x+8
To find the roots/zeros we need to factor the equation:
-x2 - 2x +8 = 0
-(x2 + 2x - 8) = 0
-(x + 4)(x - 2) = 0
x + 4 = 0; x - 2 = 0
x = -4 x = 2
(-4, 0) (2, 0)
200
Which of the following represents the following equation rewritten in vertex form?
f(x) = x2 − 14x + 7
Question options:
f(x)= (x−7)2 + 7
f(x) = (x+7)2 − 42
f(x) = (x−7)2 − 42
f(x) = (x−14)2 − 42
x2 - 14x = -7
-14/2 = -7, (-7)2 = 49
x2 - 14x + 49 = -7 + 49
(x - 7)2 = 42
f(x) = (x - 7)2 - 42
200
What is the average rate of change of the function f(x) = x2 + 4x − 5 over the interval [1,5]?
Question options:
14
5
10
11
f(1) = 12 + 4(1) - 5 = 0
when x = 1, y = 0
f(5) = 52 + 4(5) - 5 = 40
when x = 5, y = 40
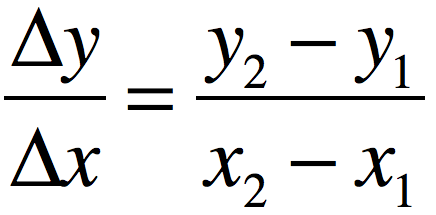
(40-0) / (5-1) = 40/4 = 10
the average ROC over the interval [1, 5] is 10
300
Using the function f(x)= −(x+2)2 + 4, and the graph chosen above, determine the following:
1. Vertex
2. Min/Max (choose one)
3. Axis of Symmetry
4. Domain
5. Decreasing Interval
1. a(x - h)2 + k = −(x+2)2 + 4
Vertex = (h, k)
Because h is negative so we have to switch the sign of 2, it would be -2, k stays the same. the vertex is (-2, 4)
2. This graph has a maximum, maximum is the y value of the vertex so it would be y = 4
3. Axis of symmetry is the x-value of the vertex so it would be x = -2
4. Domain is all real numbers
5. In this graph, decreasing is the right side so we would write it as (#, ∞). Since the AOS is -2, the decreasing interval would be (-2, ∞)
300
Covert the following functions into standard from:
1. f(x) = -3(x + 5)(x - 1)
2. f(x) = (x + 12)(x + 4)
1. -3(x2 - x + 5x - 5)
= -3x2 + 3x - 15x +15
= -3x2 - 12x + 15
2. x2 + 4x + 12x + 48
= x2 + 16x + 48
300
Find the average ROC over the interval [-2, -1] for f(x) = x2 + 3x
f(-2) = (-2)2 + 3(-2) = -2
when x = -2, y = -2
f(-1) = (-1)2 + 3(-1) = -3
when x = -1, y = -3
(-3 - 2) / (-1 - (-2) = -5/1 = -5
the average ROC over the interval [-2, -1] is -5
400
Which function represents the parabola shown in the accompanying graph?
Question options:
f(x) = (x+1)2 − 3
f(x) = −(x−3)2 −3
f(x) = −(x−3)2 + 1
f(x) = −(x+3)2 + 1
The answer is f(x) = −(x+3)2 + 1 because the vertex of this function (-3, 1) matches the vertex on the graph.
400
Covert the following functions into intercept from:
1. f(x) = x2 + 13x + 40
2. f(x) = 4x2 - 8x - 12
1. 8 x 5 = 40; 8 + 5 = 13
= (x + 8)(x + 5)
2. 4(x2 - 2x - 3)
1 x (-3) = -3; 1 + (-3) = -2
= 4(x + 1)(x - 3)
400
Find the average ROC over the interval [1, 3] for f(x) = 2x2 + 8x + 11
f(1) = 2(1)2 + 8(1) + 11 = 21
when x = 1, y = 21
f(3) = 2(3)2 + 8(3) + 11 = 53
when x = 3, y = 53
(53 - 21) / (3 - 1) = 32/2 = 16
the average ROC over the interval [1, 3] is 16
500
Using the function f(x) = x2 − 6x + 2, and the graph chosen above, find the following:
1. Vertex
2. Axis of Symmetry
3. Range
4. Y-Intercept
5. Increasing Interval
1. To find the vertex we can change it into the vertex form but we have a graph here so it's faster to look at it. Since the vertex is the highest/lowest point on a graph so in this function it would be (3, -7)
2. AOS is the x-value of the vertex. AOS is x = 3
3. To find the range, first we need to determine the maximum/minimum line, the minimum is -7 so the range would be written as: y ≥ -7 or [-7, ∞)
4. Y-intercept is the c value in the function which is 2 so the y-intercept is (0, 2)
5. Increasing is the right side and the AOS is 3 so the increasing interval would be (3, ∞)
500
Covert the following function into vertex from:
f(x) = -2x2 - 4x + 3
f(x) = a(x - h)2 + k
a = a
h = -b/2a
h = -(-4) / 2(-2) = 4/-4 = -1
k = -2(-1)2 - 4(-1) + 3 = 5
f(x) = -2(x + 1) + 5
500
Find the average ROC over the interval [2, 4] for f(x) = 4x2
f(2) = 4(2)2 = 16
when x = 2, y = 16
f(4) = 4(4)2 = 64
when x = 4, y = 64
(64 - 16) / (4 - 2) = 48/2 = 24
the average ROC over the interval [2, 4] is 24