Solving Systems of Linear Equations
Systems Again?
Linear Inequalities
When Will I Use This?
Potpourri
100
What is the solution?
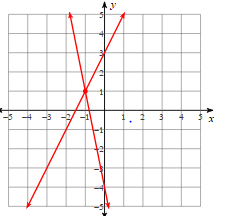
(-1,1)
100
Solve the systems of equations below:
8x +5y = 24
y = x + 10
(-2, 8)
100
With a linear inequality, the solid line means this.
The solution can be on the line
100
The difference of two numbers is 3. Their sum is 13.
Find the numbers.
5 and 8
100
Solve the systems of equations below:
-6x - 10y = 4
6x + 10y = -4
Infinitely Many Solutions
200
How many solutions are there?
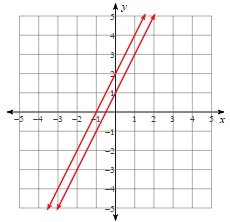
No Solutions
200
Solve the systems of equations below:
14x + 2y = 26
-14x - 6y = -50
(1, 6)
200
With a linear inequality, the dashed line means this.
Solution is NOT included, but represents the boundary line for the solutions
200
There is a collection of 60 coins, a mixture of nickels and dimes. The number of nickels is three times the number of dimes.
Determine the number of nickels and the number dimes in the collection.
45 nickels
and
15 dimes
200
The difference of two numbers is 4. Their sum is 12.
Find the numbers.
4 and 8
300
Solve the system of equations with the graph:
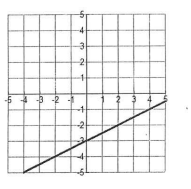
Infinite Solutions
300
Solve the systems of equations below:
-3x - 5y = 2
3x + 5y = 7
No Solution
300
In slope-intercept form, this is the linear inequality shown
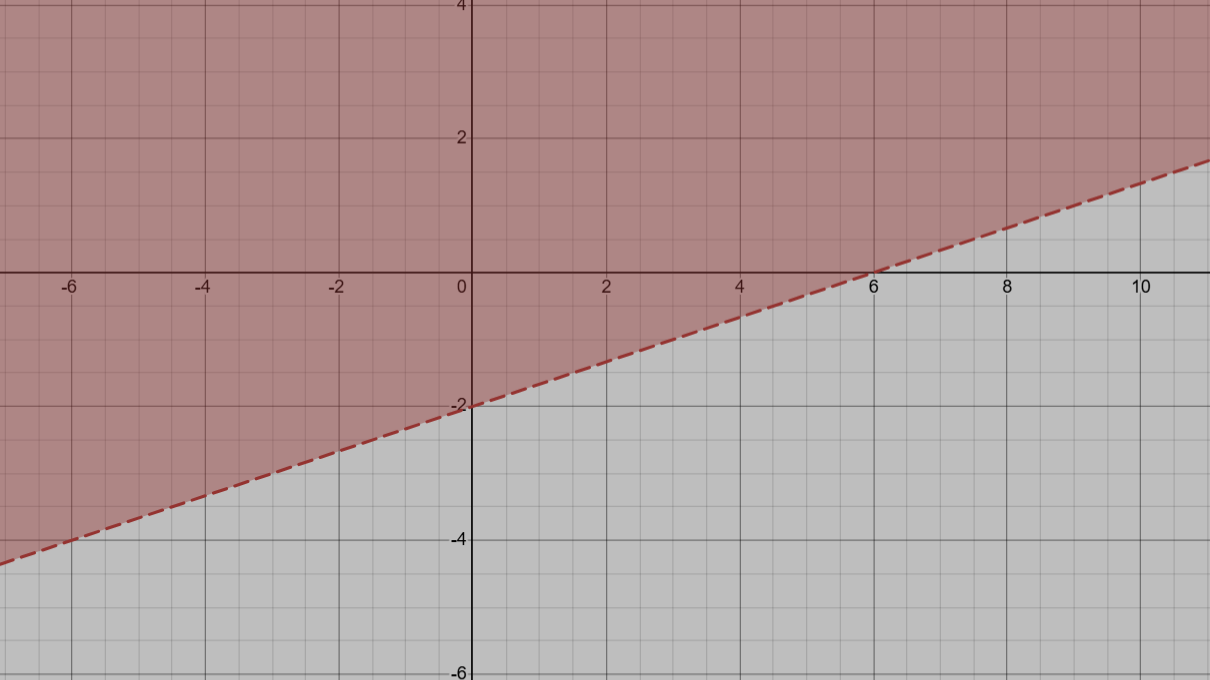
y>1/3x-2
300
For tickets at a concert, adults cost $12 and children cost $8. Assume that $960 is collected and 90 tickets are sold.
Determine the number of adults and children that attended the concert.
60 adults
and
30 children
300
In slope-intercept form, this is the linear inequality shown
y<3
400
Solve the systems of equations below:
y = -2x - 9
3x -6y = 9
(-3, -3)
400
Solve the systems of equations below:
-8x + y = -7
16x - 2y = 14
Infinitely Many Solutions
400
In slope-intercept form, this is the linear inequality shown.
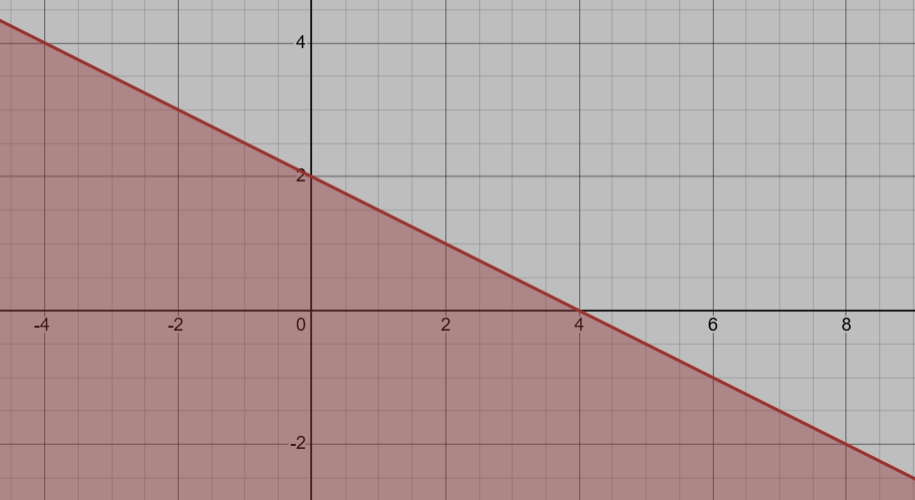
y≤-1/2x+2
400
3 small boxes of oranges and 14 large boxes of oranges costs $203.
11 small boxes of oranges and 11 large boxes of oranges costs $220.
Determine the cost of the small box of oranges and the large box of oranges.
Small box oranges: $7
Large box of oranges: $13
400
Solve the systems of equations below:
-5x - 5y = 10
y = -4x -17
(-5, 3)
500
Solve the systems of equations below:
-5x + 7y = -7
-2x - 2y = 2
(0, -1)
500
Solve the systems of equations below:
x = -8y + 2
3x + 4y = 26
(10,-1)
500
In slope-intercept form, this is the linear inequality shown.
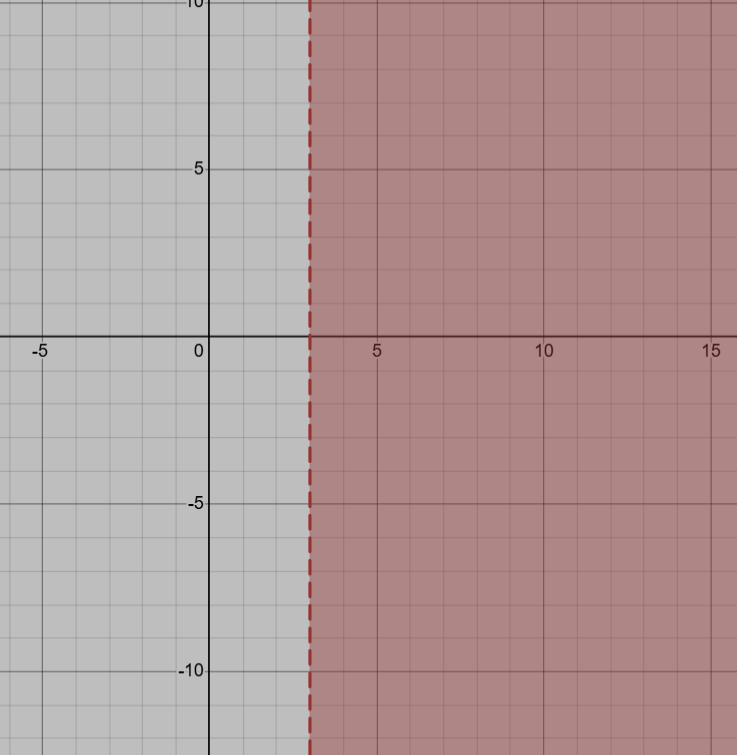
x>3
500
Car A and Car B are racing on a straight track. Car A is 10 miles ahead of Car B. Car A is traveling at a constant speed of 80 miles per hour, and Car B is traveling at a constant speed of 90 mph.
Assuming all variables remain the same, how long will it take for Car B to catch Car A?
1 hour until they meet
500
There is a collection of 123 coins, a mixture of dimes and quarters. The number of dimes is three more than four times the number of quarters.
Determine the number of dimes and quarters in the collection.
99 dimes
and
24 quarters