Graphing Quadratics
Scenarios
Operations with Quadratics
Miscellaneous Topics
100
Give a possible equation for the pictured function.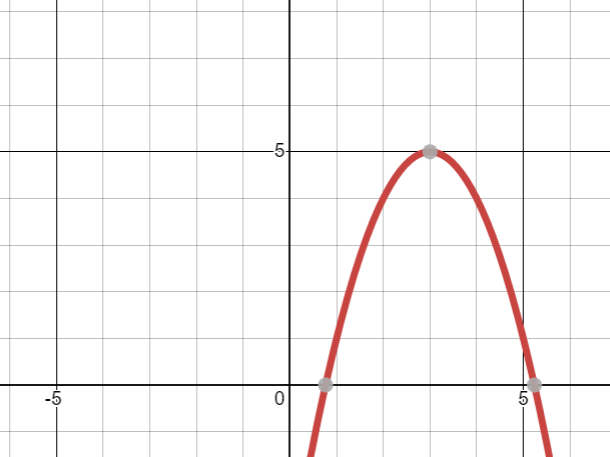
y=-(x-3)^2+5
100
Find the volume of a cube that has a side length of
2x-1
8x^3-12x^2+6x-1
100
Multiply this expression and write it in standard form:
(x+4)(x-7)
x^2-3x-28
100
Multiply:
(4x-5)(4x+5)
16x^2-25
200
What would be the vertex for the following Quadratic Function?
y=-(x-4)^2+3
Vertex = (4, 3)
200
A parking lot has an area of
2x^2+9x-5
square meters. Use factoring to find *possible* dimensions of the parking lot.
(x+5)(2x-1) meters
200
Simplify this expression and write it in Standard Form
-(x-3)^2+2
-x^2+6x-7
200
Multiply
(2x-3)^2
4x^2-12x+9
300
What would be the axis of symmetry of the Quadratic
y=3x^2-12x+40
x=2
300
Artificial turf costs $15/wq ft to install. Write a quadratic function that represents the cost of installing artificial turf on a square plot with a side length of
(x-3)
feet.
y=15(x-3)^2
or
y=15x^2-90x+135
300
Write this product in Standard Form
(4x-3y)(5x+y)
20x^2-11xy-3y^2
300
Factor the expression
x^2-13x-48
(x-16)(x+3)
400
Describe the graph of the Quadratic:
y=-1/2(x+3)^2+3
Vertex at (-3,3); pointed downwards, axis of symmetry x = -3, stretched by a factor of 2
400
An astronaut on the moon throws a moon rock into the air. The rock's height, in meters above the moon's surface x seconds after it is thrown can be determined by the function
h(x)=-1.6(x-2.5)^2+15
. What is the maximum height of the rock above the moon's surface?
15 meters
400
Find the GCF between these monomials
14x^3y^8, 84x^5y^4, 21xy^5
7a^2b^2(7a^3b-2+5ab^3)
400
Which option(s) in this list is/are linear in nature?
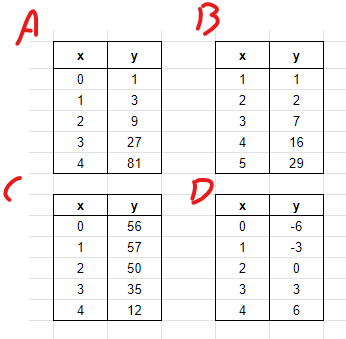
D is Linear. Common difference of 3
500
Describe the graph of the following quadratic:
y=2x^2-4x+10
Vertex at (1,8); y-intercept at (0,10); pointed upwards; compression by a factor of 2; no x-intercepts
500
Find the volume of the figure provided
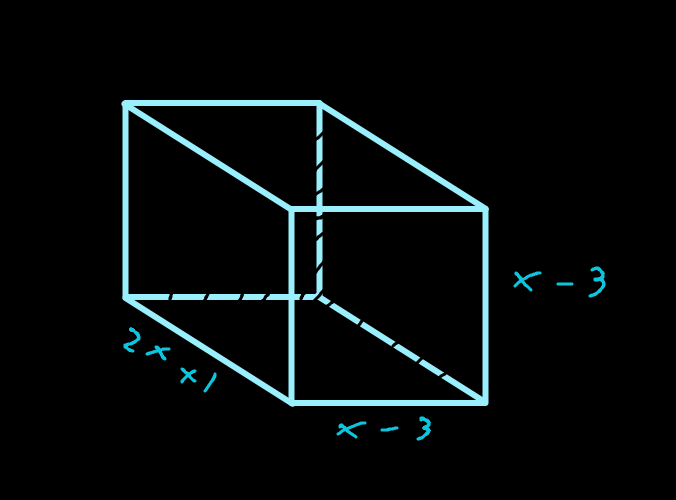
2x^3-11x^2+12x+9
500
Factor this expression
49a^5b^3-14a^2b^2+35a^3b^5
7a^2b^2(7a^3b-2+5ab^3)
500
Which relationship(s) in this list is/are Quadratic?
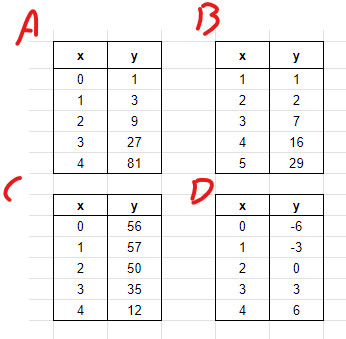
B and C