Unit 4 Quadratics Review Jeopardy Template

geometric applications

Writing/Solving Quadratics

quadratics in context

Misc

transformations

100

A painting has an area of 4 square feet. The width of the painting is two less than a number, and its length is 1 more than the same number.

Write and solve a quadratic equation to find the value of x, the width, and the length.

x = 3

width = 1

length = 4

100

Assuming that red tiles represent negative terms, what algebraic expression do the above algebra tiles represent?

A. -2x² - x + 6
B. 2x² - x + 6
C. 2x² + x - 6
D. 2x² - x - 6

B. 2x² - x + 6

100

A rock is thrown from a height of 48 feet.

Solving the quadratic equation 0=−16x²+32x+48 will give the time, x, when the rock hits the ground. Assume the rock is thrown when x = 0.

Use the graph of the equation to decide if each zero is a solution to this problem.

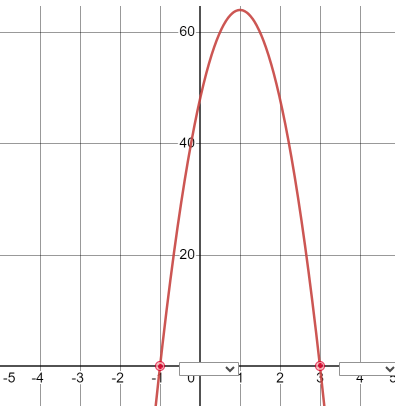A. Negative Zero is a solution

B. Positive zero is a solution

C. Both zeroes are a solution

B. Positive zero is a solution

100

Let f(x) = 3x2 − 6x + 2. Find f(2).

A. 2
B. 8
C. 10
D. 12
E. 16

A. 2

100

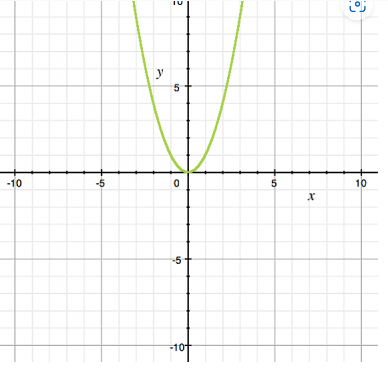
Which equation would shift the parabola down 3 units?

A. y = x²
B. y = x² - 3
C. y = x² + 3
D. y = (x+3)²

B. y = x² - 3

200

The base of a triangle is represented by (2x − 6) and the height by (x − 2). Which polynomial expression BEST represents the area of the triangle?

A. x² + 5x + 6
B. x² − 5x + 6
Cx² − 5x − 6
D. 2x² + 10x + 122
E. 2x² − 10x − 12

B. x² − 5x + 6

200

Solve for x.
x² − 16 = 9

A. x = 3 or −3
B. x = 4 or −4
C. x = 5 or −5
D. x = 6 or −6
E. no solution

C. x = 5 or −5

200

At Mariana's last art market, she sold 100 prints priced at $15 each. She determines that for each dollar increase in price, she will sell 4 fewer prints. From this information, she writes the function R(n)=(15+n)(100−4n) to represent the revenue she will receive with n $1 increases in the price.

Rewrite the function in a form that reveals the vertex.

A. R(n)=−4n²+40n+1500
B. R(n)=−4(n−5)²+1600
C. R(n)=−4(n−10)²+1900

B. R(n)=−4(n−5)²+1600

200

If f(x) = 3x2 – 12x + 4, find f(–2).

A. -40
B. -20
C.20
D. 40
E. 60

D. 40

200

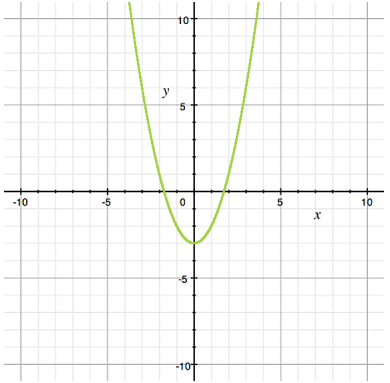
Which equation is graphed?

A. y = (x+3)²
B. y = (x-3)²
C. y = x² - 3
D. y = x² + 3

C. y = x² - 3

300

Coach Luna is designing a rectangular practice field for elementary soccer and kickball. The length of the practice field is 6 yards longer than its width, as shown in the image.

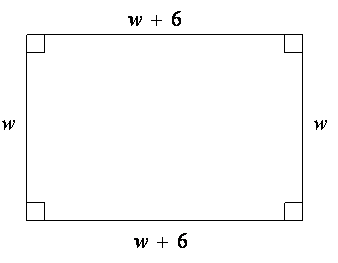
If w²+6w−187=0 represents a valid relationship for this practice field, then what quantity could the 187 represent?

A. the perimeter of the practice field

B. the length of the diagonal of the practice field

C. the area of the practice field

D. the area of one of the triangles formed by the diagonal of the practice field

C. the area of the practice field

300

Solve the quadratic equation.

(x+1)2 = 16

A. x = 3 or -5
B. x = -3 or 5
C. x = ±5
D. x = ±1
E. x = 4 or -4

A. x = 3 or -5

300

Identify the vertex and determine what it represents in the context of Mariana's art prints.

Responses

A. The vertex is (5, 1600). Mariana's revenue will be maximized when she sells the art prints for $5. The maximum revenue is $1600.
B. The vertex is (5, 1600). Mariana's revenue will be maximized when she increases the price by $5 to $20. The maximum revenue is $1600.
C. The vertex is (10, 1600). Mariana's revenue will be maximized when she sells the art prints for $10. With this price, she will sell 1600 art prints.
D. The vertex is (5, 1475). Mariana's revenue will be maximized when she sells the art prints for $5. The maximum revenue is $1475.The vertex is (5, 1475).
E. The vertex is (5, 1475). Mariana's revenue will be maximized when she increases the price by $5 to $20. The maximum revenue is $1475.

B. The vertex is (5, 1600). Mariana's revenue will be maximized when she increases the price by $5 to $20. The maximum revenue is $1600.

300

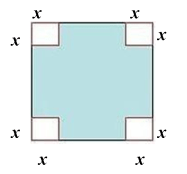
Beginning with a square sheet of cardboard with 8-inch sides, Hannah is going to cut square corners out and then fold up the flaps to make an open box. If x is the length of the sides of the square corners, then the area of the base of her box will be A(x)=4x²−32x+64.

What is the most reasonable domain for this function, in this situation?

A. {x: 0 ≤ x < 4}
B. {x: 0 ≤ x < 8}
C. {x: 0 ≤ x < 16}
D. {x: 0 ≤ x < 32}

A. {x: 0 ≤ x < 4}

300

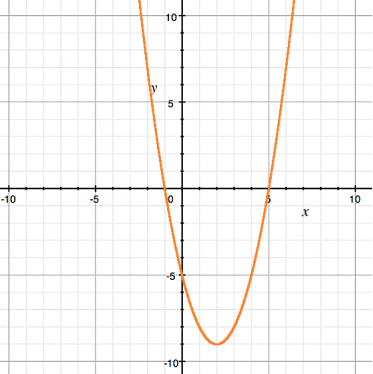
The function whose graph is shown is

A. f(x) = x² - 5
B. f(x) = x² - 9
C. f(x) = x² + 5
D. f(x) = x² - 4x - 5

D. f(x) = x² - 4x - 5

400

Jinwon wants to put a basketball hoop in his backyard. He will create a square concrete section in the corner of his yard where he can practice basketball. The dimensions of his yard are shown in the diagram above.

The expression x²+13x+30 can be used to represent the area of the entire yard.

What does the 13x+30 in the expression represent?

A. The area of the basketball court
B. The perimeter of the yard
C. The perimeter of the yard that does not include the basketball court
D. The area of the yard that does not include the basketball court

D. The area of the yard that does not include the basketball court

400

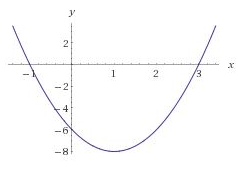
Use the intercepts and extreme value to find an equation for the quadratic function.

Af(x) = 2x² - 3x - 6
Bf(x) = 3x² - 4x - 6
Cf(x) = 2x² - 4x - 6
Df(x) = 2x² - 4x + 6

Cf(x) = 2x² - 4x - 6

400

The concentration, in parts per million, of a type of antibiotic in a human's bloodstream after h hours can be modeled by the polynomial function C(h) = −0.09h² + 3.5h + 8. What is the concentration of the antibiotic after 3 hours in parts per million to the nearest hundredths?

A. 17.69
B. 18.77
C. 38.69
D. 42.34
E. 52.66

A. 17.69

400

Find the average rate of change for f(x) = x² + 7x + 10 from x = −5 to x = 2.

A. 2
B. 4
C. 8
D. 14

B. 4

400

What is the function g(x) created from f(x) = x² by moving the graph left 4 units, vertically stretching it by a factor of 5, and shifting the graph down 8 units?

A. g(x) = 4(x+5) + 8
B. g(x) = 5(x−4)2 + 8
C. g(x) = 8(x+4)2 + 5
D. g(x) = 5(x+4)2 − 8

D. g(x) = 5(x+4)2 − 8