Vocabulary
Graphs
Quadratics
Division & Zeros
Complex #s
100
A shortcut for long division
Synthetic division
100
Write the end behavior in function notation:
as x-->inf, f(x) -->inf
as x-->-inf, f(x) -->-inf
100
State the vertex:
y = (x+3)2 - 5
(-3, -5)
100
Divide x4 - 4x3 - 7x2 + 34x - 24 by x+3 using synthetic division
x3 - 7x2 +14x - 8
100
Simplify:
sq root(-24)
2i sq root(6)
200
The directions that a graph goes as you look to the left and right
End behavior
200
Deg: Even or Odd?
LC: Pos or Neg?
Even, Positive
200
Re-Write in Vertex Form:
f(x) = x2 + 10x + 14
f(x) = (x+5)2 - 11
200
Divide 6x3 + 23x2 + 24x + 7 by 3x+7 using long division
2x2 + 3x + 1
200
Simplify:
-5 + 8i - (8 - 6i)
-13 + 14i
300
Name three synonyms for "root" of a polynomial equation.
Solution
Zero
X-intercept
300
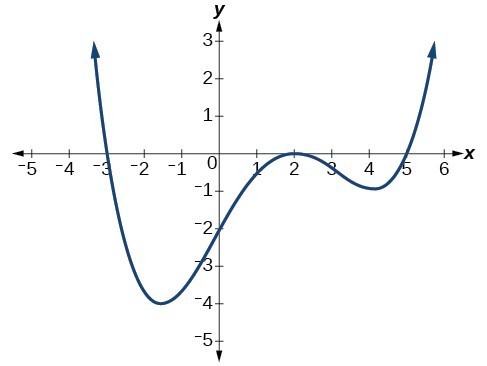
State the roots and multiplicities
x=-3, x=2 mult 2, x=5
300
Write in standard form:
y = 3(x-7)2 - 4
y = 3x2 -42x + 143
300
Divide 2x5 - 14x3 + 24x - 24 by x-3 using synthetic division
2x4 + 6x3 + 4x2 +12x + 60 + 156/x-3
300
Simplify: 5i * 2i
-10
400
The number of times a factor appears in a polynomial.
Example: In the polynomial y=(x+4)2(x - 3), the factor (x+4) has a _______________ of 2.
Multiplicity
400
Write a possible equation in factored form for the polynomial shown:
y=(x+3)(x+2)(x-1)
400
Solve:
7x2 = -224
x = +/- 4i sq root 2
400
One solution of the polynomial y=x3+8x2+5x-14 is x=-2. Find ALL zeros!
x = -2, -7, 1
400
Simplify:
(3 + 2i)2
5 + 12i
500
The _________________ _____________ Theorem helps you determine a list of possible solutions for a given polynomial function.
The Rational Root/Zero Theorem
500
Write a possible equation in factored form for the polynomial shown: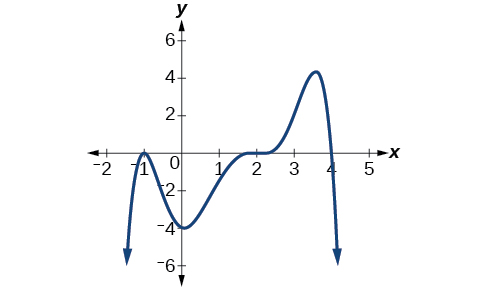 
Note: LC must be negative!
y = -(x+1)2(x-2)3(x-4)
500
Solve:
4x2 - 4 = -24
x = +/- i sq root 5
500
Given that x-2 and x+3 are both factors of the polynomial 2x4 + 7x3 - 4x2 -27x -18, find the remaining FACTORS.
(x -2)(x + 3)(2x + 3)(x + 1)
500
Simplify:
-2i(4 - 7i) - 7(-6 -7i)
28 + 41i