Rolle with It &
Mean It
Mean It
It's Critical
Pitch Perfect
Second Chances
Reach for the Pinnacle
100
State the criteria that must be met to apply the Mean Value Theorem?
What is:
1. The function is continuous on the closed interval [a,b]
2. The function is differentiable on the open interval from [a,b]
100
Find all the critical numbers for the function
f(x)=x^3-12x^2
What are 0 and 8?
100
Find the value of x at which the function
f(x)=1/(1+x^2)
change from increasing to decreasing?
What is
0
100
State the criteria must be met to determine a maximum using the second derivative test on a given differentiable function.
What is
f'(x)=0
f"(x)<0
100
Which point on the graph of
y=sqrtx
is closest to the point (5,0) ?
Hint think distance formula
What is
(9/2, sqrt3/2)
200
State the criteria that must be met to apply Rolle's Theorem.
1. The function must be continuous on the closed interval from [a,b].
2. The function must be differentiable on the open interval from (a,b).
3. f(a)=f(b)
200
Find all the critical numbers of the function
f(x)=root(3)(9-x^2)
What are:
-3, 0, 3
200
Find the interval on which
f(x)=x-2sinx
is increasing over the interval
[0,2pi]
What is
[pi/3, (5pi)/3]
200
Find the x-coordinate of the point of inflection of the function
f(x)=x^3-x^2-x+1
What is
1/3
200
An open box is made from a 16in x 16in piece of cardboard by cutting equal squares from each corner and folding the sides up, For the maximum volume, what size squares should be cut out?
What is
8/3 *8/3
300
Given the following function state whether or not MVT can be applied over the interval [-1,3] and if so find "c".
f(x)=(x^2-2x-3)/(x+2)
What is
Yes
c= 1
300
Find all critical numbers for the function
f(x)=(x-1)/(x+1)
What is:
There are no critical numbers.
300
What is the length of the interval on which the function
f(x)=x^3-3x^2-9x
is decreasing?
What is
4
300
What is the y-coordinate of the point of inflection of the function
f(x)=x^3-3x^2
What is
-2
300
A revenue function is given by
R(x)=6000x-0.2x^3
where x is the number of units sold. Find the number of units x that produces maximum revenue.
What is 100
400
Use the graph of f to estimate the values of c that satisfy the Mean Value theorem for the interval [0,4]
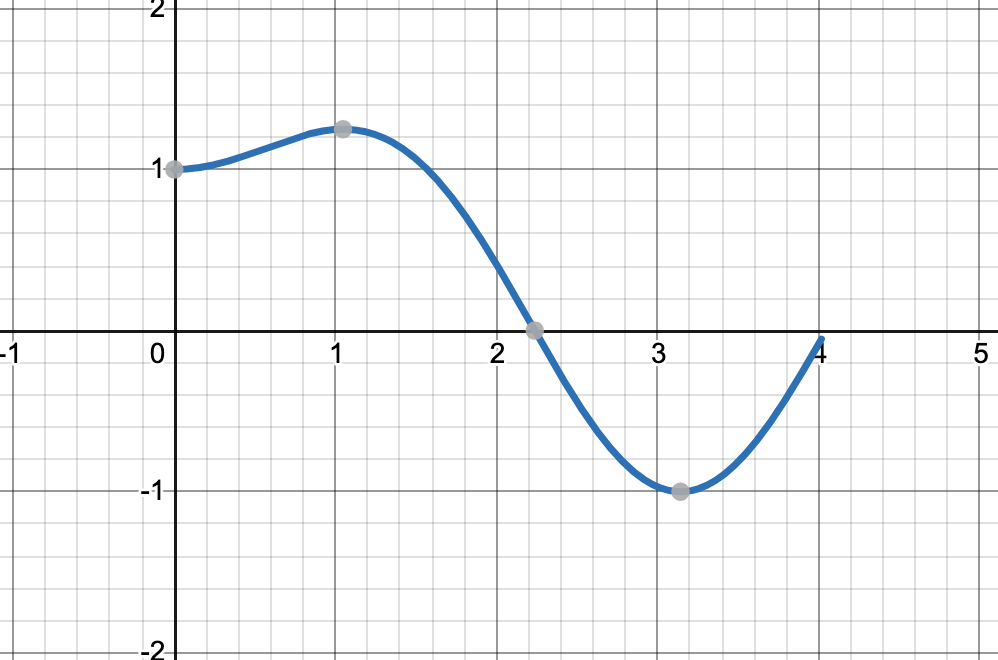
What is:
1.2 or 3.1
400
Find the distance between the two critical number of the function:
x^3-3x+27
What is 2
400
State the intervals over which
f(x)=x^4-6x^2
is increasing and decreasing.
What is
increasing:
(-sqrt3,0)uu(sqrt3,oo)
decreasing:
(-oo,-sqrt3)uu(0,sqrt3)
400
How many points of inflection does the function
f(x)=x^4-4x^3+6x^2
have.
What is
0
400
What is the smallest positive slope for a tangent line to the graph of
y=2x^3-2x^2+5x+1
What is
13/3
500
If f(x) is continuous over the closed interval [1,4] and differentiable on the open interval (1,4), and that
f'(x)<=5
for all x in [1,4]. If f(1)=2 what is the maximum, possible value that f(4) can be.
What is
17
500
Given that
f(x)=x^3+ax^2+bx
has critical numbers at x=1, and x=3, find a and b.
What are
-6, 9
500
Consider the function
f(x)=sin^2x+cos x
What is the interval over which the function is increasing when
0<=x<=2pi
What is
(0,pi/3) and (pi,5pi/3)
500
Find the interval on which the function
f(x)=ln(x^2+1)
is concave upward.
What is
(-1,1)
500
The total cost of producing x widets per day is
$(1/4x+35x+25)
and the price per set at which they must be sold is
$(50-1/2x)
what should be the daily output to obtain a maximum total profit?
What is
10 units