Find the value of x.
x = 14

Which type of point of concurrency is this and what type of line segment forms it?
Orthocenter formed by three altitudes.
Find the centroid of the following.
A(1,8) B(7,19) C(10,0)
(6,9)
GE is 11, find AE and AG
AE is 33
AG is 22
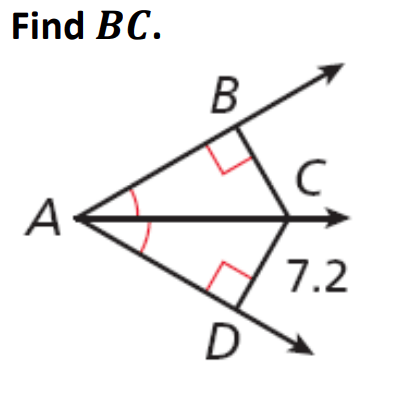
BC = 7.2
What is the definition of a midsegment and its properties
A line that goes from midpoint to midpoint and is parallel to the opposite side and half the length of the parallel side
 Which point of concurrency is this and what type of line forms it?
Which point of concurrency is this and what type of line forms it?
Centroid formed by three medians.
Find the incenter.
A(-5,2), B(7,-3), C(-5,-3)
(-3,-1)
If G is the centroid and BF is 18 and BG is 2x, find x and BG.
Find BD.
22
Find the value of x and y.
y = 24
x = 14

Which type of point of concurrency is this and which line segment forms it?
Circumcenter formed by three perpendicular bisectors.
Where does the orthocenter and circumcenter fall in an obtuse triangle (150)
Where does orthocenter fall on a right triangle(150) Specifically where?
Where does circumcenter fall on a right triangle(150) Specifically where?
Where does orthocenter and circumcenter fall in acute triangles(150)
Outside
On the right angle
on the midpoint of the hypotenuse
inside the triangle
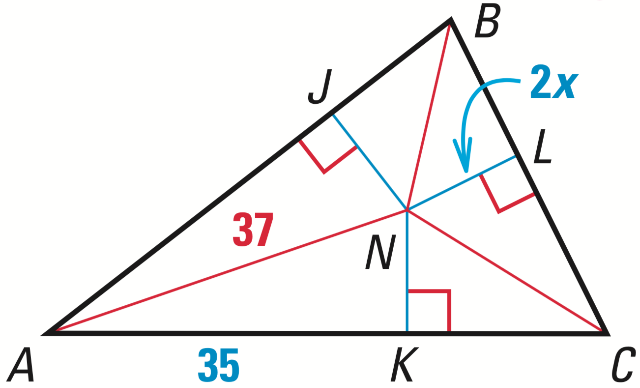
N is the incenter of the triangle. If AK = 35, AN = 37, and NK = 10. Find x.
x = 5.

Find AD.
AD = 104
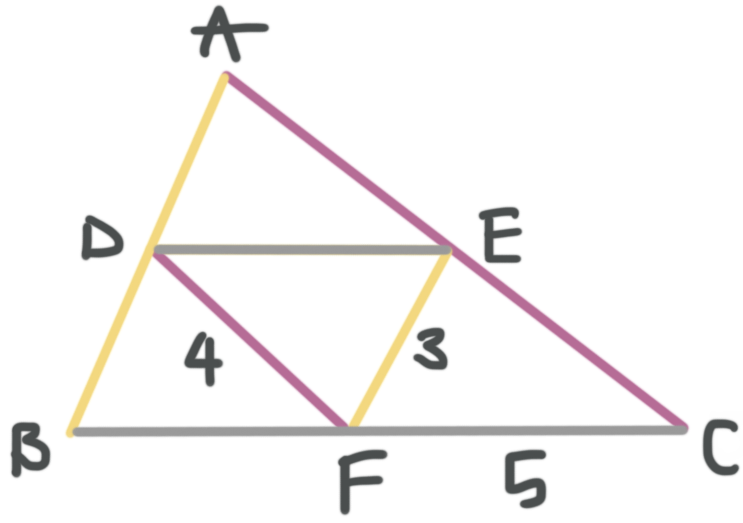
Find the value of AC, DE, and AB.
AC = 8
DE = 5
AB = 6
![]()
Which type of point of concurrency is this and what type of line segment forms it?
Incenter formed by three angle bisectors.
Find the orthocenter of the following
A(1,2)B(-5,2)C(-2,-2)
(-2,-0.25)
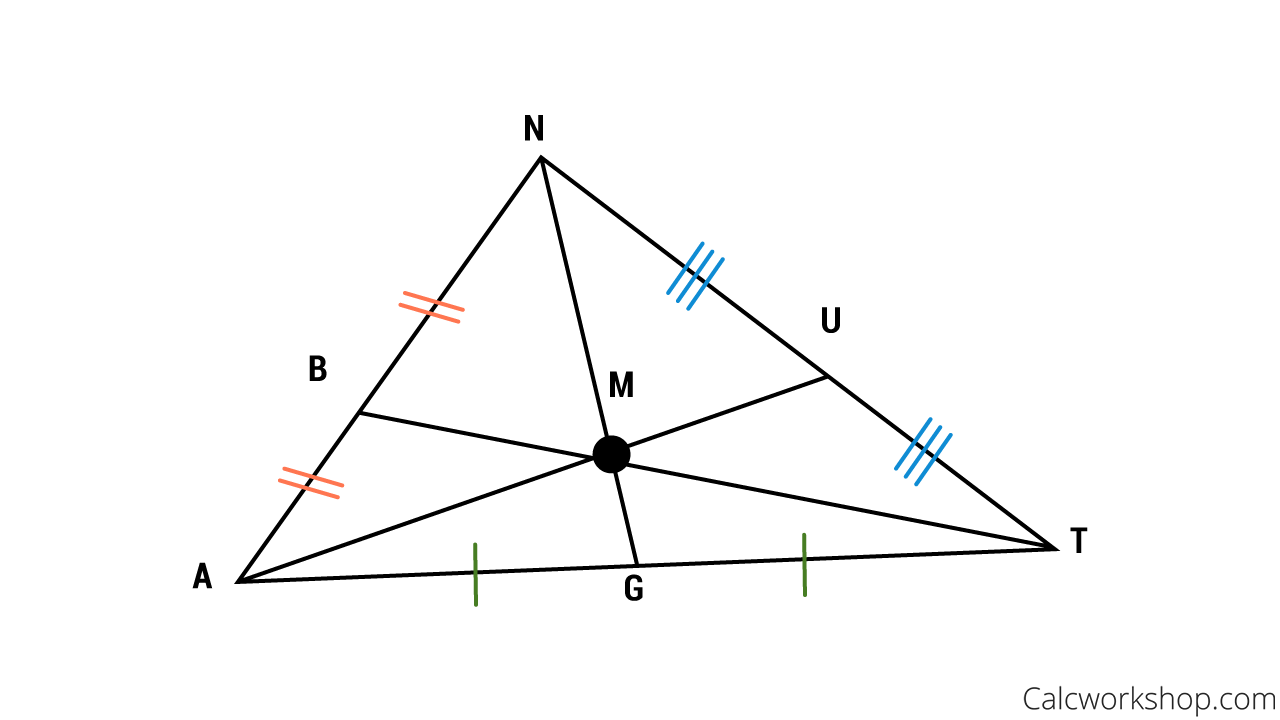
M is the centroid of the triangle. If GM is 5, find GN and NM.
GN = 15
NM = 10
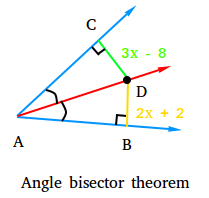
Find x and y if XZ is a perpendicular bisector of WY. and XZ is an angle bisector of WZY
x = 5
y = 4
in Triangle ABC. This midpoint of AB is D and the midpoint of BC is E. If DE is
x^2+6x-5
and AC=22 find the value(s) of x
x=-8 and 2
Both work.

Angle bisector - BG
Altitude - BH
Median - BD
Perpendicular Bisector - DE
Find the circumcenter of the following
A(0,0),B(4,2),C(2,6)
Midpoints and slopes are
AB(2,1) slope:1/2
BC(3,4) slope: -2
AC(1,3) slope: -2
(1,3)

N is the circumcenter of this triangle. Find x and y.
x = 4
y = 3

Find <AYB.
90