Midsegments
Points of Concurrency
Inequalities
Points of Concurrency Math
Bisectors
100
Find the value of x.
x = 14
100
Which type of point of concurrency is this and what type of line segment forms it?
Orthocenter formed by three altitudes.
100
If AE is 3x and GE is 11, find AE and x.
AE is 33 and x is 11.
100
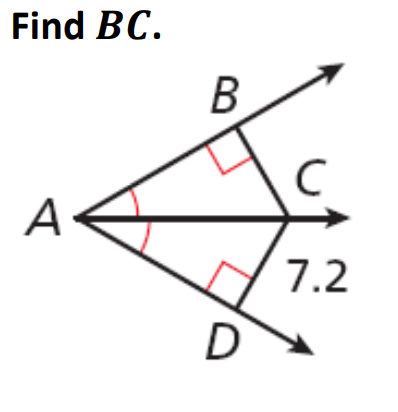
BC = 7.2
200
Which point of concurrency is this and what type of line forms it?
Centroid formed by three medians.
200
Which of these combinations forms a triangle?
a) 3, 4, 5
b) 3, 3, 6
c) 2, 3, 5
a) 3, 4, 5
200
If G is the centroid and BF is 18 and BG is 2x, find x and BG.
BG is 12 and x is 6.
200
Find BD.
22
300
Which type of point of concurrency is this and which line segment forms it?
Circumcenter formed by three perpendicular bisectors.
300
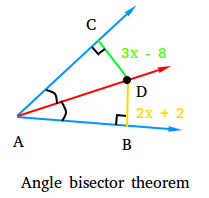
What is a possible value for x?
2 < x < 18
300
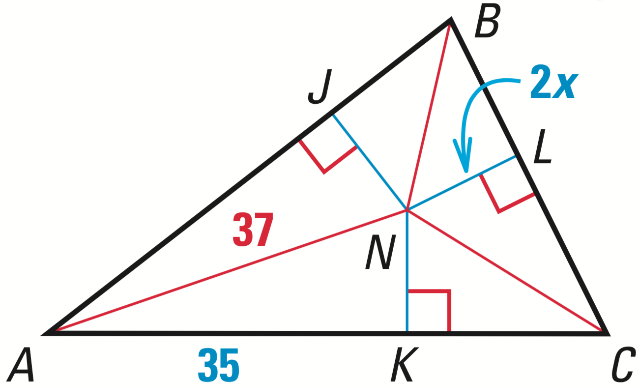
N is the incenter of the triangle. If AK = 35, AN = 37, and NK = 10. Find x.
x = 5.
300
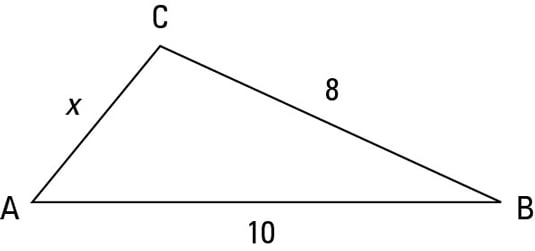
Find AD.
AD = 104
400
Find the value of x and y.
y = 24
x = 14
400
Which type of point of concurrency is this and what type of line segment forms it?
Incenter formed by three angle bisectors.
400
Order the sides from least to greatest.
AC < BA < BC
400
Find x and y if XZ is a perpendicular bisector of WY.
x = 5
y = 4
500
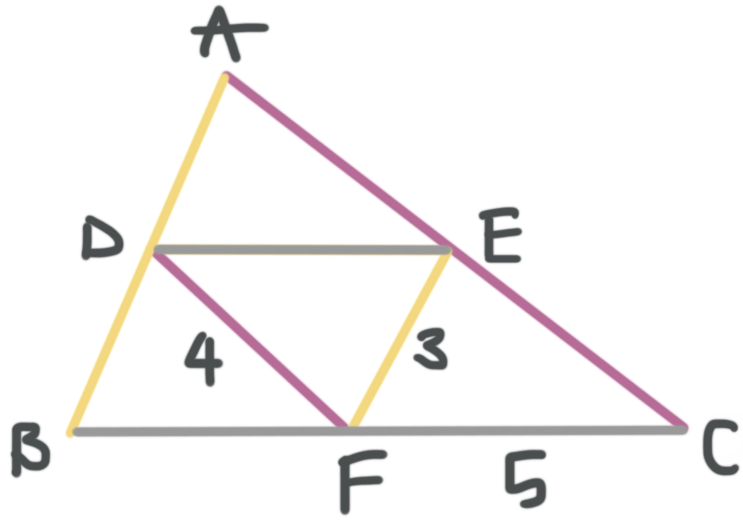
Find the value of AC, DE, and AB.
AC = 8
DE = 5
AB = 6
500
Angle bisector - BG
Altitude - BH
Median - BD
Perpendicular Bisector - DE
500
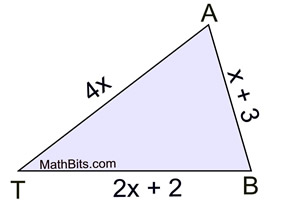
If the perimeter of the triangle is 40, is this triangle able to be constructed?
No, the sides would be 20, 12, and 8 which do not form a triangle.
500
N is the circumcenter of this triangle. Find x and y.
x = 4
y = 3
500
Find <AYB.
90