Venn Diagrams
Tree Diagrams
MCP
Independent vs Dependent
Theoretical Probability
100
Draw a venn diagram and shade P(A U B)
Shade both circles including intersection
100
Probability red, then blue
3/4 * 1/4 = 3/16
3/16 or 0.1875
100
You want to design a 30-minute workout. For the first 15 minutes, you will choose an aerobic exercise from running, kickboxing, or circuit training. For the second 15 minutes, you will work on strengths and/or balance choosing from weight training, TRX, Bosu, resistance bands or your core routine. How many such workouts are possible?
3*5 = 15 workouts
100
Determine if the events are independent or dependent.
You pick out a sock from your drawer, put it on and grab another sock from the drawer
Dependent
100
A bag contains 10 red marbles, 8 blue marbles and 2 yellow marbles. Find the theoretical probability of getting a blue marble.
8/20 = 2/5 = 0.4 or 40%
200
P(Internet)
9 + 26 = 35
35/50 = 0.70
200
Probability of picking blue, then green.
1/5 * 4/5 = 4/25
4/25 or 0.16
200
You brought 7 shirts, 4 shorts, 8 socks, and 3 shoes on vacation. Everything is neutral colors so they can match. How many outfit combinations can you make?
7 * 4 * 8 * 3 = 672 outfits
200
Determine if the events are independent or dependent.
You roll two number cubes and get doubles.
Independent
200
What is the theoretical probability of selecting a queen from a standard deck of cards?
4/52 = 1/13 = 0.077
300
Draw a Venn diagram to describe the following.
Suppose that 530 students play soccer, 290 students play basketball, and 130 students play both sports. There are a total of 1500 students at the school.
Just soccer - 400
Intersection - 130
Just basketball - 160
Neither sport - 810
300
Find the probability of being on time to both classes.
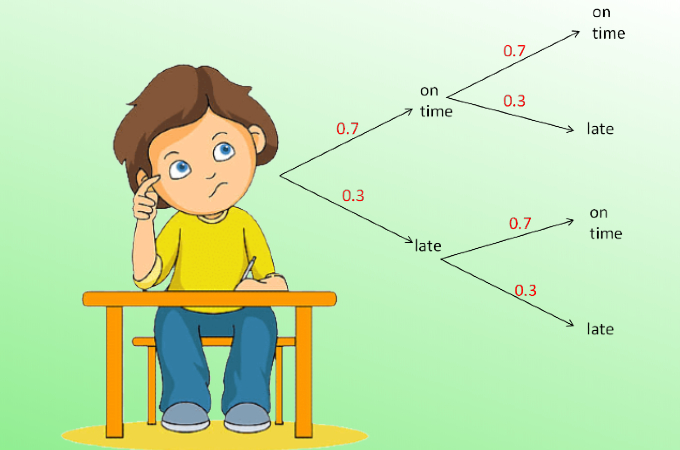
0.7 * 0.7 = 0.49
300
How many ways can the letters of the word TRIANGLE be arranged?
8 * 7 * 6 * 5 * 4 * 3 * 2 * 1 = 40,320 ways
300
Use the definition of independence to determine if the events are independent.
P(A) = 3/10
P(B) = 5/10
P(A and B) = 3/20
3/10 * 5/10 = 0.15
3/20 = 0.15
Independent events
300
What is the probability of selecting a king or queen from a standard deck of cards, putting it back, and selecting another king or queen?
8/52 * 8/52
2/13 * 2/13
4/169 = 0.0237
400
P(Cats)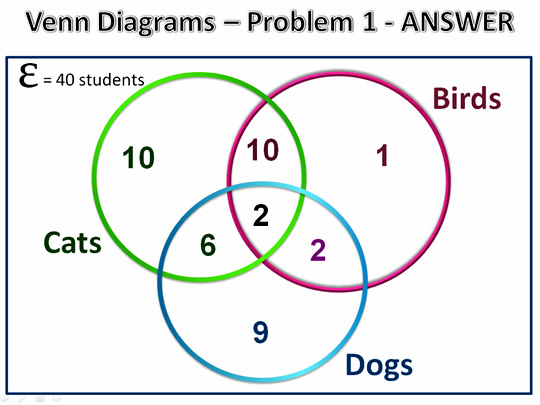
10 + 10 + 6 + 2 = 28
28 + 9 + 2 + 1 = 40
28/40 = 0.7 or 70%
400
Probability of throwing a strike.
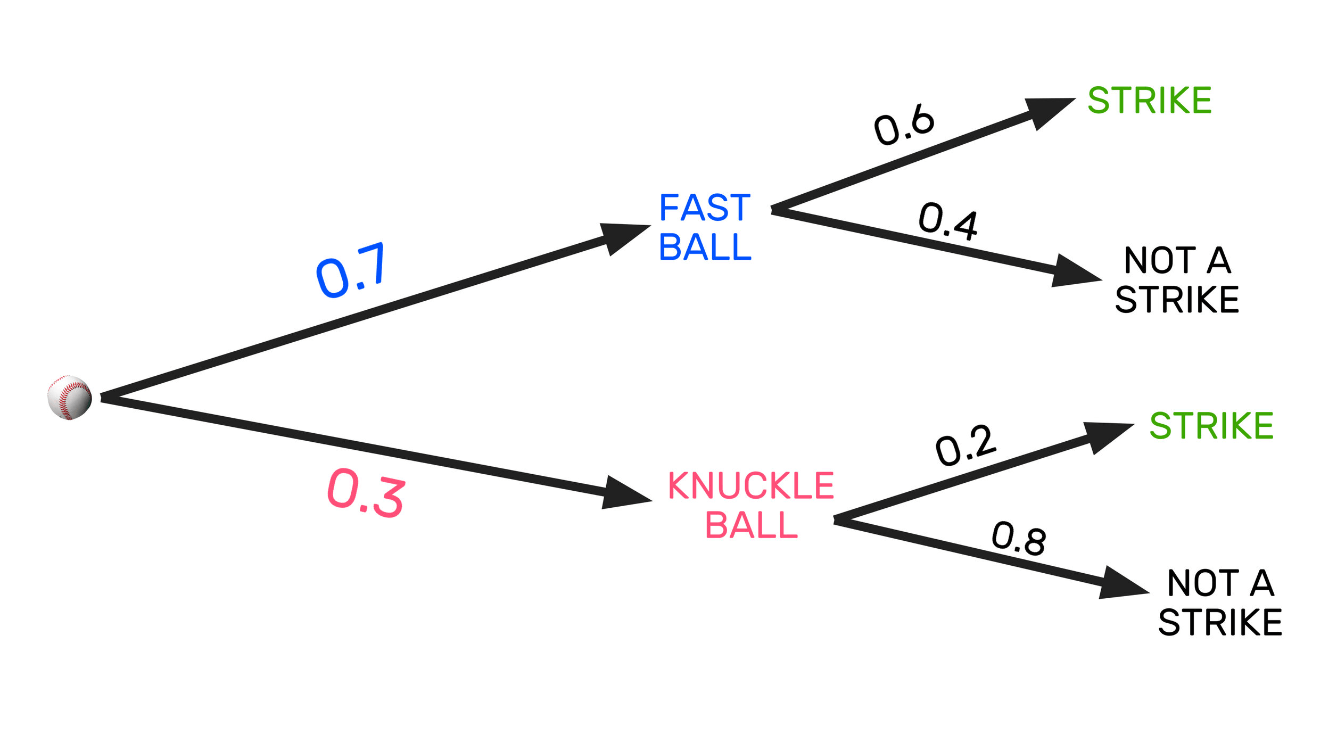
0.7 * 0.6 + 0.3 * 0.2
0.42 + 0.06
0.48
400
How many license plates, consisting of 2 letters followed by 4 digits, are possible if we do not want to repeat any letters or numbers?
26 * 25 * 10 * 9 * 8 * 7
= 3,276,000 plates possible
400
Use the definition of independence to PROVE the events are independent. (show the math)
P(heads)
P(rolling a 6 on a cube)
P(heads) = 1/2
P(rolling a 6 on a cube) = 1/6
P(heads and 6)= 1/12
1/2 * 1/6 = 1/12
400
What is the probability of selecting an ace from a standard deck of cards, putting it aside, and selecting another ace?
4/52 * 3/51
12/2652
1/221 = 0.0045
500
In a survey of university students, 64 had taken mathematics course, 94 had taken chemistry course, 58 had taken physics course, 28 had taken mathematics and physics, 26 had taken mathematics and chemistry, 22 had taken chemistry and physics course, and 14 had taken all the three courses. Find how many take only math.
(Create a three way Venn diagram)
28 - 14 = 14
64 - 14 - 14 - 12 = 24 students
500
P(Win at least one match)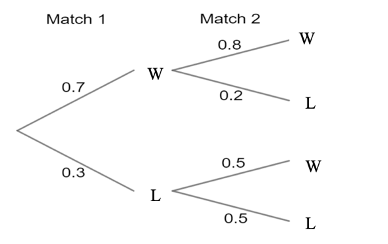
Win both: 0.7 * 0.8 = 0.56
Win, then lose: 0.7 * 0.2 = 0.14
Lose, then win: 0.3 * 0.5 = 0.15
0.56 + 0.14 + 0.15 = 0.85 or 85%
500
A phone number in the area consists of 10 digits. The first three digits are the area code 301. The next 7 digits are selected at random. How many combinations are possible if we do not reuse 3, 0 or 1?
7 * 7 * 7 * 7 * 7 * 7 * 7 = 823, 543 combinations
500
Use the definition of independence to test if the events are independent.
P(A) = 2/5
P(B) = 1/3
P(A and B) = 1/4
2/5 * 1/3 = 2/15
2/15 does not equal 1/4
Not independent
500
What is the theoretical probability that two random people share the same birthday (month and day)?
1/365
(technically 1/365.25)