What is the difference between a hole in a graph and a vertical asymptote?
Vertical asymptote is a restriction on the denominator that cannot be cancelled out
Find the hole of the rational function below.
((x-1)(x-4))/((x-4)(x+2))
(-4, 1/2)
The equation of the horizontal asymptote of y = 3/x
y = 0
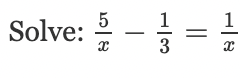
x=12
The equation of a rational functions with two vertical asymptotes at x=3 and x=-5
Answers Vary
(x+5) and (x-3) in denominator
Find the hole of:
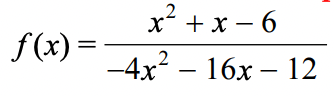
(3,1/2)
The equation of the horizontal asymptote of this function
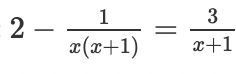
x= -1/2 and 1
Answers Vary
Ex)
(x-4)/(x-2)
Find the hole of:
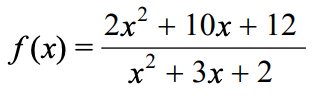
(-2,-2)
The equation for the horizontal asymptote of the following graph
y = 1
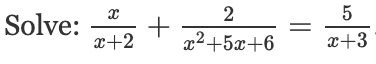
x= 4
(-2 is extraneous)
Write a rational function with a vertical asymptote at x=3
Answers vary
Ex)
(2(x+1))/(x-3)
Graph the function below. Label all asymptotes, intercepts, and holes.
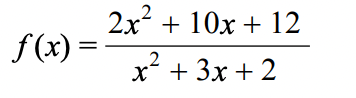
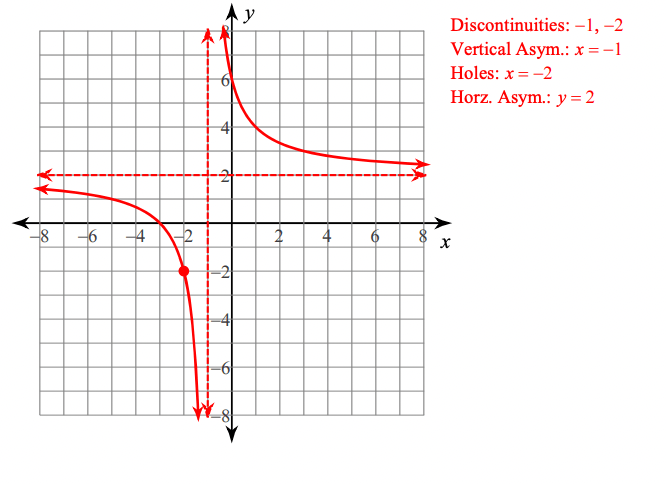
The horizontal asymptote of
(x-2)/(3x+4)
y = 1/3
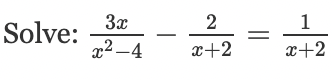
No solution!
Write a rational function that has a hole when x=-1 and a vertical asymptote at x=3
y= ((x+1)(x-2))/((x+1)(x-3)
How is a hole created and how do I find it?
A hole is created when a factor is canceled out of the numerator and denominator of a rational function. This creates a "hole" in our graph at an (x,y) point.
The horizontal asymptote of (x-2)/(x-3)
y = 1