Probability Distribution
Binomial Distribution
Geometric Distribution
Combining Distributions
Miscellaneous
100
True or False:
The probability distribution of a continuous random variable cannot be described graphically.
False
100
True or False:
An important requirement for a random variable to be binomial is where there are multiple possible outcomes.
False
100
Which of the following statements is incorrect about geometric distributions:
a. Trials are independent
b. There can only be two possible outcomes
c. Defined as a continuous probability distribution
d. Can have an indefinite number of trials
c. Defined as a continuous probability distribution
100
Given two probability distributions X and Y, to find the variance of X+Y you can add the variance of X plus the variance of Y.
True
(Not true for standard deviation)
100
In order for something to be a probability distribution, what conditions must be satisfied?
All probabilities must be between 0 and 1 inclusive, the sum of probabilities must be 1.
200
What is the missing probability of the following probability distribution?
0 - 0.12
1 - 0.16
2 - 0.24
3 - 0.32
4 - x
5 - 0.05
The missing probability is x = 0.13
200
The probability that a school soccer team will win is 0.6.
What is the probability of losing 3 matches out of 5?
The probability they will lose 3 matches out of 5 is 0.2304
200
Explain how to find the expected value of a geometric distribution.
Divide 1 by the probability of success on each trial.
200
The number of questions I answer a day can be modeled with a normal distribution where the mean is 190 and the standard deviation is 100. I want to know how many questions I can expect to answer in a school week (5 days).
950 questions
200
A die is tossed 5 times.
What is the probability of getting exactly 2 fours?
The probability of getting exactly 2 fours is 0.161 or 16%
P(x) = 5C2 (0.167)2 (0.833)3
300
Identify which of the two events are discrete or continuous probability distributions.
Explain the difference between the two distributions.
Event A: The number of thunderstorms per year
Event B: Amount of ice in a tea glass
Event A: discrete probability
Event B: continuous probability
Differences: Discrete distribution is countable while continuous is measurable
300
Consider the following statement:
You flip 4 coins two times and count the number of times the coins land tails.
How do you know this can be modeled with a binomial distribution?
Binary - Only two possible outcomes
I - Trials are independent (one trial will not affect the outcome of the following trials)
n is fixed
Probability of success is constant
300
Explain the difference between a geometric distribution and a binomial distribution.
Binomial: has a fixed amount of trials before it begins and X number of successes obtained in that fixed number.
Geometric: has a fixed number of successes and counts the number of trials needed to obtain that first success. Can have an indefinite number of trials.
300
The number of questions I answer a day can be modeled with a normal distribution where the mean is 190 and the standard deviation is 100. I want to know the standard deviation for a school week of 5 days. What is the condition that must be satisfied to use the formula?
Each day must be independent of the next.
300
Which of the following events is Geometric
Event A: Random selection of members for a team from a group of boys and girls
Event B: Asking a group of people if they chose the letter A or B on a test until you find someone who chose the letter in favour.
Event B
400
Find the expected value of the following probability distribution:
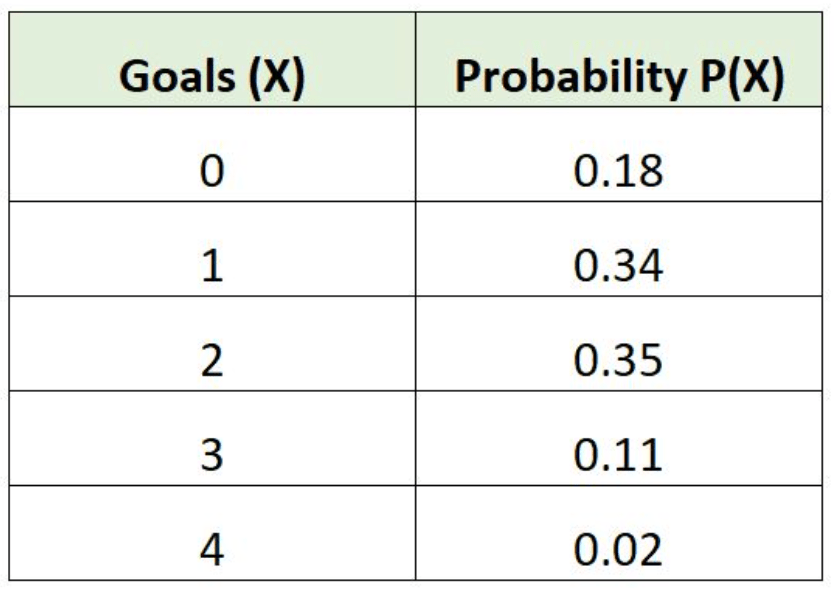
The expected value is E(x)= 1.45
400
The probability that you might grab a red M&M out of a bag of M&Ms is 20%.
If there are 24 M&Ms, what is the probability of selecting at least 4 red M&Ms (with replacement)?
The probability of finding at least 4 M&Ms is 0.46 or 46%
400
A baseball player has a batting average of 0.32, which is also the probability that he gets a hit each time he is batting.
What is the probability that he gets his first hit in his third position at bat?
The probability that he gets his first hit in his third position at bat is 0.1480 or 15%
P(x) = (1-0.32)3-1 0.32 = 0.1480
400
The number of questions I answer a day can be modeled with a normal distribution where the mean is 190 and the standard deviation is 100. I want to know the standard deviation for a school week of 5 days. Assume each day is independent of the previous day.
223.6 questions
400
Can this be modeled with Binomial Distribution? Why or why not?
You shake a bag of 3,000 names of raffle entries and draw a group of 15 winners out without replacement.
Yes, since it is binary, has a fixed p, fixed n and satisfies the 10% condition
500
You pay $1 for a ticket to roll a 6 sided die.
If you roll 1, 2, 3 or 6 you lose. If you roll a 4 you get your money back. If you roll 5, you win $4.
Will you win or lose more money?
What is a fair price for this game?
The expected value is negative, therefore, you will lose more money
A fair price for this game would be $0.83
E(x) = -0.16667 or -$16.6
Fair price = 1 - 0.16667 = 0.8333 or $0.83
500
The probability of a telesales representative making a sale is 0.15.
They need to achieve an expected value of 5 sales per day.
What is the least number of calls each day a representative should make to achieve this requirement?
The representative should make at least 3.33 or 4 calls to have a good chance of meeting this requirement.
500
In MDM4U, 27% of students enjoy eating peas.
Let X = the number of students encountered before the first student who enjoys peas is found.
What is the expected number of students who enjoy peas?
The expected number of students who enjoy peas is 2.7037
500
The number of questions I answer a day can be modeled with a normal distribution where the mean is 190 and the standard deviation is 100. Assume each day is independent. What is the probability that I answer over 1,200 questions a week?
z=1.12
13.3%
500
10% of applicants for a job at Mcdonald's have the right skills. The manager interviews the applicants one at a time until they find the right candidate.
What is the probability the right candidate is found in the first 10 applicants?
0.6513